Lesson 3 Homework Practice Area Of Trapezoids Answer Key

Hey there, math explorers and curious minds! Ever feel like you're staring at a worksheet and thinking, "What in the world am I supposed to do with this?" You're not alone! Sometimes, those homework assignments can feel like a puzzle, and when it comes to finding the
You know those days when you're just chilling, maybe scrolling through your phone, and you stumble upon something that makes you go, "Ooh, that's interesting!"? Well, that's kind of the vibe we're going for here. We're not talking about super-duper advanced calculus, but rather a friendly peek into "Lesson 3 Homework Practice: Area of Trapezoids." And specifically, we're going to chat about that magical thing called the
Unpacking the Trapezoid: More Than Just a Funny Shape
So, what exactly is a trapezoid, anyway? If you picture a regular rectangle or square, they’re all neat and tidy with parallel sides everywhere. A trapezoid is a bit more… adventurous. It’s a four-sided shape, a quadrilateral, where at least one pair of opposite sides is parallel. Think of it like a tabletop that’s a little wonky, or a slice of a pyramid.
Why does this matter? Well, understanding shapes is like understanding the building blocks of the world around us. From the design of a bridge to the shape of a garden plot, geometry is everywhere! And trapezoids, with their slightly slanted sides, pop up in some surprising places.
The Big Question: How Do We Measure It?
Okay, so we've got our trapezoid. Now, how do we figure out how much space it takes up? This is where the "area" part comes in. Area is basically the measure of the 2D space inside a shape. Imagine you wanted to tile a floor in the shape of a trapezoid – the area tells you how many tiles you'd need.
The formula for the area of a trapezoid might look a little intimidating at first glance. It often involves adding up the lengths of the two parallel sides (which we call bases), multiplying that sum by the height (the perpendicular distance between the bases), and then… dividing by two! It’s like saying, "Let's get a sense of the average width, stretch it out, and then see how much space it covers."
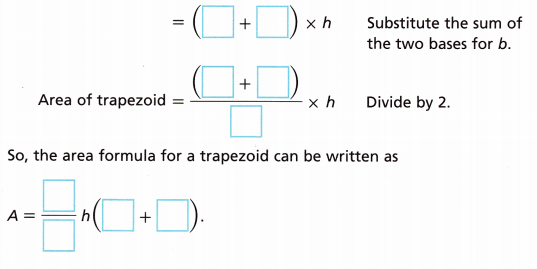
Think of it this way: if you took two identical trapezoids, flipped one upside down, and stuck them together along their slanted sides, you'd create a parallelogram. And the area of a parallelogram is pretty straightforward: base times height. Since the trapezoid is essentially half of that combined shape, that's where the "divide by two" comes in!
The Glorious Answer Key: Your Homework Buddy
Now, let's talk about that "answer key" part of "Lesson 3 Homework Practice: Area of Trapezoids." For many of us, the answer key is like a secret weapon in the battle of homework. It's that helpful friend who gives you a little nudge in the right direction or confirms that, yes, you absolutely nailed it!
When you’re working through those practice problems, it’s easy to get stuck. Maybe you’re unsure if you’ve correctly identified the bases, or perhaps the height seems tricky to pinpoint. That’s where the answer key shines!

It’s not about just copying the answers, oh no. The real magic of an answer key is in its ability to serve as a
When Things Don't Quite Add Up…
But what if your answer doesn't match the key? Don't throw your pencil across the room in frustration! Instead, think of it as an opportunity to become an even better mathematician. This is where the curiosity really kicks in!
Take a deep breath. Go back to the problem. Reread the question. Did you use the correct formula? Did you plug in the right numbers? Was there a calculation error? Sometimes, it’s a simple slip-up, like a misplaced decimal point or a forgotten addition.

Comparing your work to the answer key, and understanding how they arrived at that answer, is like having a private tutoring session. You can see where your thinking might have diverged and learn from it. It’s like following a recipe – if your cake doesn't turn out as expected, you go back to the recipe to see where you might have missed a step or added too much of something.
Why It's Cool (Seriously!)
So, why is all this trapezoid talk and answer key checking actually cool? Because it’s about
Trapezoids themselves are surprisingly versatile. Think about the sides of a slide at a playground – those are often trapezoids! Or the shape of a ramp. Even some types of roofs have trapezoidal elements. Understanding how to calculate their area helps us in real-world applications, from construction to design.

And that answer key? It’s not just a list of solutions. It’s a
The Joy of Understanding
There’s a real sense of accomplishment that comes from understanding a concept, especially one that initially seemed a bit puzzling. When you can look at a trapezoid, identify its bases and height, apply the formula, and arrive at the correct answer (perhaps after a little help from the answer key), you’ve achieved something!
It’s like finally figuring out how to assemble a piece of furniture. At first, the instructions look like hieroglyphics, but with a bit of patience and maybe checking a diagram, suddenly, it all clicks, and you have a sturdy bookshelf! That feeling of "Aha!" is incredibly satisfying.
So, the next time you’re faced with "Lesson 3 Homework Practice: Area of Trapezoids," don’t just see it as a chore. See it as an adventure! Embrace the challenge, use that answer key as your trusty guide, and enjoy the process of discovery. You might be surprised at how much you learn, and how much you actually enjoy it!
