Lesson 2 Skills Practice Complementary And Supplementary Angles

Hey there, geometry explorers! Ever feel like math class is a bit of a snooze-fest? Well, get ready to have your mind tickled, because we're diving into something seriously fun: Lesson 2 Skills Practice: Complementary and Supplementary Angles. Don't let the fancy names scare you off. Think of it like a secret handshake for shapes, and once you know it, a whole new world of cool connections opens up.
Imagine you've got a pizza. You cut it in half, right? That's two nice, big slices. Now, what if you take one of those halves and cut it again, but this time you make two perfectly even pieces? You've just created some angles! And guess what? Some of those angles are buddies, and they have special relationships. It's like having a dynamic duo in the world of lines and corners.
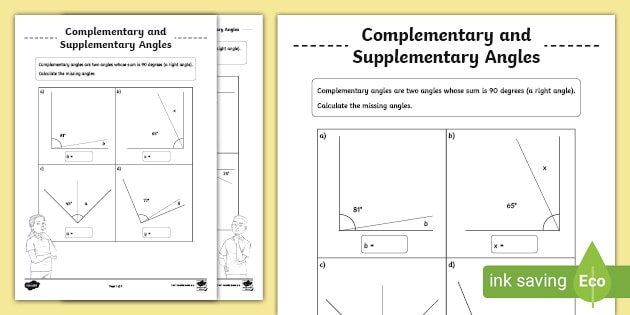
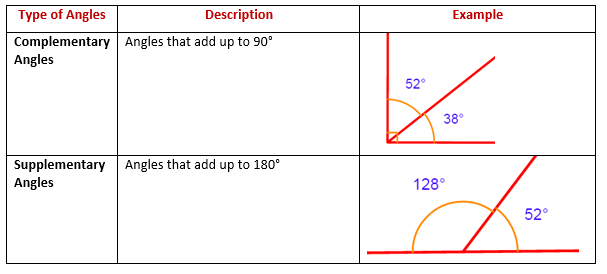
Let's talk about the first superstar pair: Complementary Angles. These guys are like the ultimate tag-team partners. They’re two angles that, when you smoosh them together, add up to exactly 90 degrees. Think of a perfect corner, like the one on a book or a square tile. That’s a 90-degree angle. Now, imagine you draw a line right through that corner. Boom! You’ve just split that perfect corner into two smaller angles. If those two smaller angles add up to 90 degrees, they're complementary. It's like they complete each other’s mission to form that right angle. Pretty neat, huh?
What makes this so cool? Well, it’s all about prediction and discovery. Once you know that two angles are complementary, you can instantly figure out the missing piece! If you know one angle is, say, 30 degrees, and you know it’s complementary to another angle, you can do some quick math in your head: 90 - 30 = 60. That other angle has to be 60 degrees. It’s like solving a mini-puzzle. No guessing involved, just pure, elegant math magic. It’s surprisingly satisfying to see how these simple relationships unlock answers.
Now, let’s meet the other power couple: Supplementary Angles. These two are a bit more chill. Instead of aiming for a neat 90-degree corner, they’re all about making a straight line. Yep, two angles are supplementary if they add up to a grand total of 180 degrees. Imagine a straight road. That's a straight line, 180 degrees of pure straightness. If you have a point on that road and draw a line upwards from it, you've just created two angles that sit next to each other along that road. If those two angles add up to 180 degrees, they are supplementary. They're like the best of friends who always hang out on a straight path.

Why is this so entertaining? Because it’s another simple rule that leads to big insights. If you see two angles sitting next to each other and forming a straight line, you automatically know their total. If one angle is, let’s say, 110 degrees, and you know it's part of a supplementary pair, you can quickly calculate the other: 180 - 110 = 70 degrees. That missing angle is 70 degrees, and it's not a guess; it's a mathematical certainty! This is the kind of stuff that makes you feel like a detective, uncovering hidden truths with just a little bit of knowledge. It’s the thrill of prediction and the joy of finding that perfect fit.
The Lesson 2 Skills Practice is where you get to play around with these concepts. It's not just about memorizing definitions; it's about applying them. You’ll find yourself looking at diagrams and immediately spotting these complementary and supplementary relationships. It’s like learning to see the hidden patterns in the world around you. Suddenly, the angles in a city street, the way a ladder leans against a wall, or even the slices of a birthday cake become more interesting. You start to see the math at play!
What makes this particular practice session special is its focus on real-world connection, even if it’s in a simplified way. These aren't abstract ideas floating in space. They are fundamental building blocks for understanding more complex shapes and designs. Think about architecture, art, or even video game design. All of these fields rely on precise angles and spatial relationships. By mastering complementary and supplementary angles, you’re getting a sneak peek into how things are built and designed.
It’s also about building confidence. When you can solve these angle problems, you're proving to yourself that you can tackle math. Each correct answer is a little victory, a boost to your brainpower. And the best part? It’s usually presented in a way that’s not intimidating. You’re given clear examples, and the practice problems are designed to help you solidify your understanding. It’s learning by doing, and that’s often the most effective and enjoyable way to learn.
So, if you’re looking for a way to make math a little less “meh” and a lot more “aha!”, then definitely check out the Lesson 2 Skills Practice: Complementary and Supplementary Angles. It’s a fantastic introduction to a fundamental concept that’s surprisingly fun and incredibly useful. It’s the kind of learning that makes you feel a little bit smarter and a lot more connected to the geometric world. Give it a go – you might just surprise yourself with how much you enjoy it!
