Kuta Software Infinite Algebra 1 Graphing Absolute Value Functions
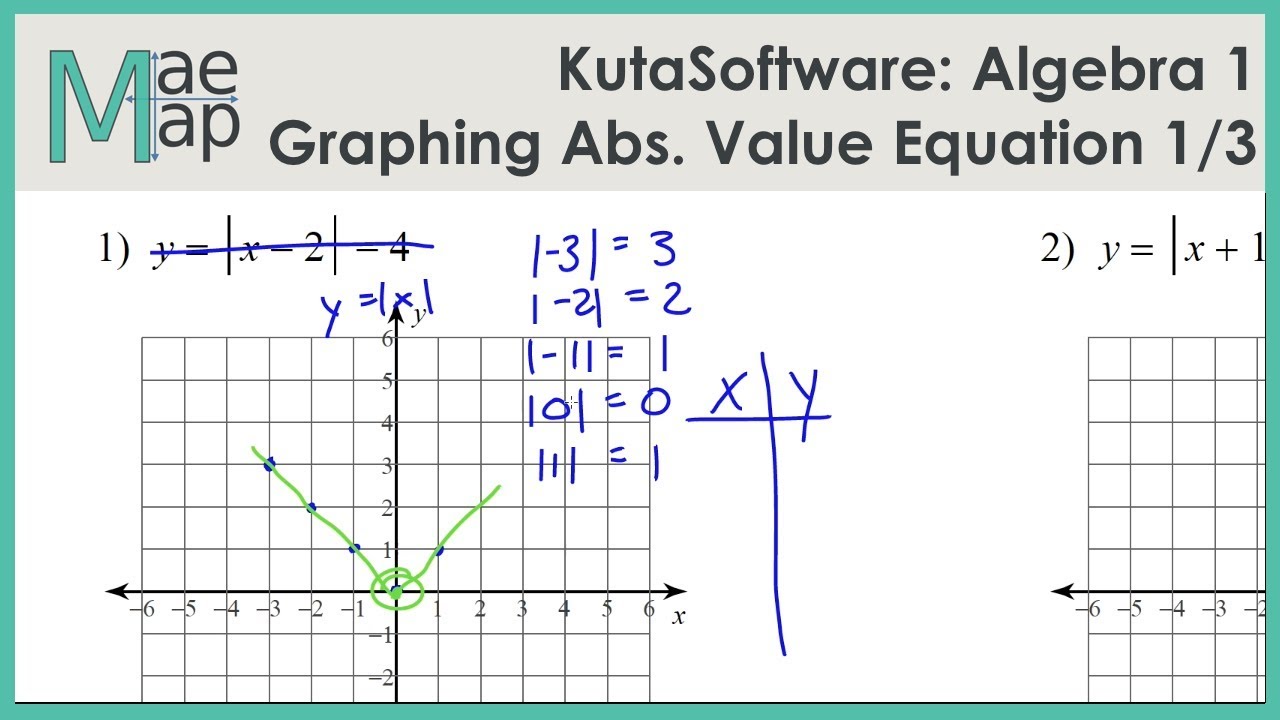
Imagine a world where numbers are a little bit quirky, a little bit dramatic, and can even do a little dance. That’s sort of what diving into Kuta Software Infinite Algebra 1 and its absolute value functions feels like. It’s like meeting a new cast of characters, each with their own special personality on the graph.
Now, we all know what a regular old function looks like, right? It’s usually a smooth, flowing line, like a gentle river. But then, BAM! Along comes the absolute value function, and it’s like the river suddenly hits a really sharp rock and has to change direction. It’s not just a bend; it’s a pointy, dramatic U-turn.
Think of the absolute value symbol, those two straight lines, like little bouncers at a club. They take any number that comes their way – positive, negative, even zero – and they tell it, "You can only be this happy, this positive!" No matter what, the number that comes out is always on the good side of the number line. It's like a magical filter.
When you plot these guys, it’s not just a line anymore. It’s a vertex, a sharp point that’s the star of the show. This vertex is where the magic happens, where the function decides to switch its mood from going down to going up, or vice versa. It’s the pivot point of all the drama.
The coolest part is how you can move these absolute value functions around. It’s like having a set of toy houses and you can slide them left, right, up, or down on your graph paper. Add a little number inside the absolute value bars, and your whole V-shape slides! It's a secret handshake with the graph.
If you see a minus sign outside the absolute value, well, that's a different kind of drama. It's like putting the whole V-shape upside down. It’s the function saying, "You know what? Let's take a flip and see things from the other side." It’s a little bit rebellious, but in a fun, predictable way.
The standard, basic absolute value function, the one that starts at the origin (0,0) and goes up in both directions, is like the "plain vanilla" of absolute value functions. It’s the foundation, the starting point for all the more exciting variations. It’s dependable and always a good place to begin understanding the concept.
But then, you start tweaking things. You add numbers inside those absolute value bars, next to the ‘x’. This is where the horizontal sliding happens. Think of it like adjusting the steering wheel on a car. You turn it a little, and the car moves left or right. Same with the graph; a change inside means a sideways shuffle.
It’s important to remember that when a number is inside with the ‘x’, and it’s added or subtracted, you have to think a little backwards. If you see (x - 3), you might think it moves to the right 3. But nope, it actually moves to the right 3! It's a little mathematical trickery, like a magician pulling a rabbit out of a hat, but the hat is the absolute value.

On the flip side, if it’s (x + 3), it feels like it should go left, and it does! It moves to the left 3. It’s like the numbers have their own secret language, and once you learn it, you can predict all their moves. The Kuta Software problems are like little puzzles that help you crack this code.
Now, what about moving up or down? That’s when you see a number hanging out outside the absolute value bars. If it’s a positive number, the whole V-shape just floats upwards. If it’s a negative number, it sinks down. It’s like the function is wearing little platform shoes or has weights attached to its feet.
These vertical shifts are the most straightforward. Add 5, and the whole graph goes up 5 units. Subtract 2, and it dips down 2 units. It’s like giving the entire drawing a gentle nudge up or down on the page. No tricky backwards thinking required here!
Sometimes, you’ll see a number multiplying the absolute value expression. This is like a squeeze or a stretch. If the number is bigger than 1, the V-shape gets narrower, more skinny. It's like someone's pulling the sides of the V closer together.
If the number is between 0 and 1, the V-shape gets wider, more spread out. It’s like the function is yawning and stretching its arms out. These stretch and shrink transformations are fascinating to watch as they change the visual character of the graph.
The combination of these movements is where the real fun begins. You can have a V-shape that’s flipped upside down, shifted left, and stretched wide all at once. It’s like creating your own unique absolute value masterpiece. The Infinite Algebra 1 exercises from Kuta Software are your palette and brushes.

Each problem is an opportunity to build a new shape, to understand how these transformations work together. It’s not just about getting the right answer; it’s about seeing the visual story unfold on the graph. You’re not just graphing points; you’re directing a little geometric play.
Think of the vertex again. It's the heart of the absolute value function. When you shift the function, you're actually just moving that vertex. All the other points follow its lead, maintaining their relative positions.
The neat thing about absolute value is that it's a reminder that even when things seem complicated, there’s often a simple, underlying structure. It’s about finding that core, that point of origin, and then understanding how everything else relates to it. It's a metaphor for life, really!
So, next time you're faced with an absolute value function from Kuta Software, don’t just see a bunch of numbers and symbols. See a shape with a personality, a function that can move, flip, and stretch. It’s a little bit of mathematical magic, ready to be explored.
The beauty of these functions lies in their predictable yet dramatic nature. They take the seemingly chaotic world of numbers and give it a clear, sharp structure. It's a delightful dance between order and visual flair, all thanks to the humble absolute value.
And the more you practice with Kuta Software, the more intuitive these movements become. You'll start to see the graph in your mind's eye before you even draw it. It's like developing a superpower for visualizing mathematical transformations.

So, embrace the V-shape! Give it a spin, slide it around, and watch it transform. It’s a simple concept with a surprisingly rich visual language, and the journey of graphing absolute value functions with Kuta Software is a truly enjoyable one.
Who knew that learning algebra could involve so much dramatic flair and visual fun? These absolute value functions are the unsung heroes of the graphing world, bringing sharp edges and exciting transformations to our mathematical adventures.
It’s a journey of discovery, where each graph tells a story of movement and change. And with Kuta Software Infinite Algebra 1, that story is always an engaging one, full of surprises and satisfying resolutions.
So, let your inner mathematician do a happy dance! These V-shapes are waiting for you to bring them to life on the graph, and the experience is anything but boring.
It’s like learning to sculpt with numbers, where the absolute value is your chisel, and the graph is your clay. You’re creating something new and exciting with every transformation!
The power of the absolute value is in its ability to bring order to chaos, transforming negative numbers into positive ones. This transformation, when applied to graphing, creates the iconic V-shape that is both simple and complex in its behavior.
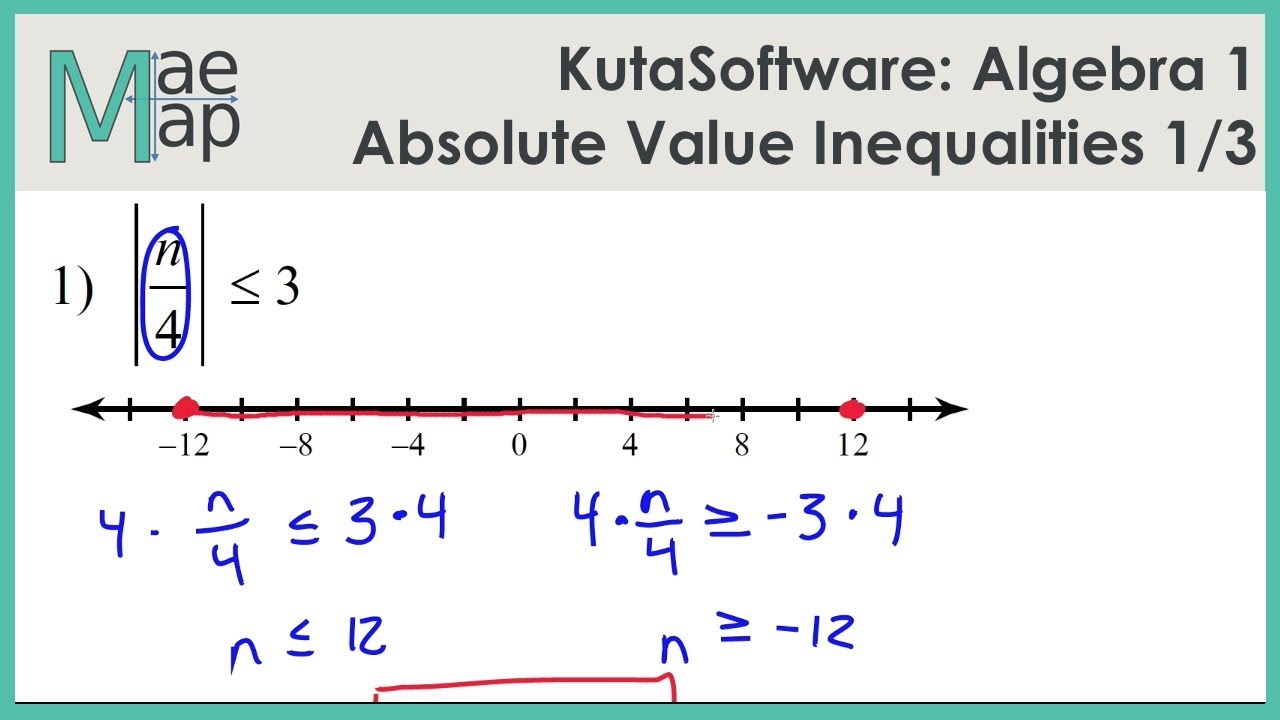
The vertex, that crucial turning point, is where the function's direction changes. It's the pivot upon which the entire graph turns, and understanding its location is key to mastering these functions.
With Kuta Software, you get a fantastic playground to experiment with all these movements. You can see firsthand how adding or subtracting from ‘x’ shifts the graph horizontally, and how changes outside the absolute value affect it vertically.
It's a truly rewarding experience to see a complex equation translate into a visually distinct and understandable graph. The absolute value function, in its elegance, provides just that.
So, have fun with it! Let the graphs be your canvas and the transformations your artistic tools. The world of absolute value functions is a vibrant and engaging place to explore.
And remember, even the most complicated-looking absolute value graph can be broken down into simple transformations of the basic V-shape. It’s all about understanding the building blocks.
This is where the magic of Infinite Algebra 1 truly shines, making abstract mathematical concepts visual and accessible.
The journey of graphing absolute value functions is a testament to the beauty and logic of mathematics, offering a delightful challenge for any learner.
