Introduction To Logarithms Common Core Algebra 2 Homework Answers
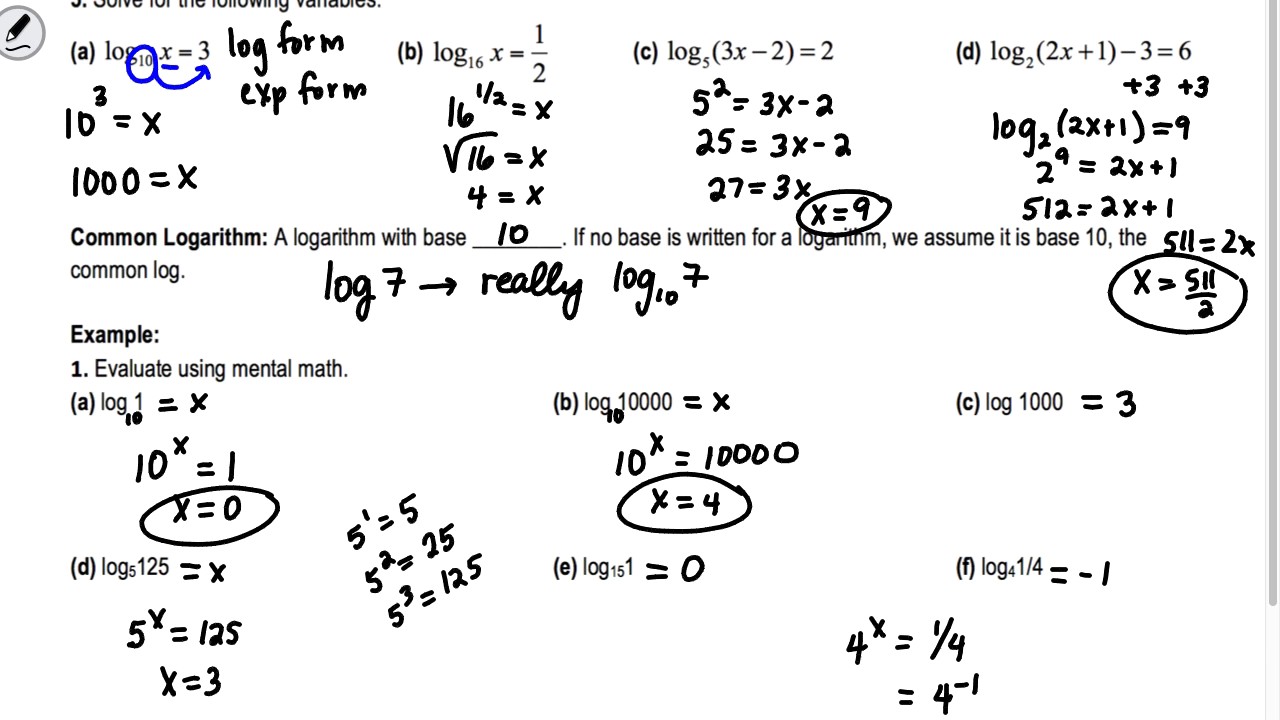
Hey there! So, you've stumbled upon the magical world of logarithms, huh? Don't worry, we've all been there. It's like, suddenly, the math teacher pulls out this whole new concept, and your brain goes, "Wait, what is that?" But seriously, logarithms are actually pretty cool once you get the hang of them. Think of them as the secret handshake to unlocking exponents. We're talking Common Core Algebra 2 homework answers here, so let's dive in, shall we?
You know how sometimes you have those "aha!" moments in math? Logarithms can definitely be one of those. They're not some mystical creature conjured up by ancient mathematicians just to mess with us. Nope, they have a real purpose, and it’s all about figuring out powers. It’s like a super-powered inverse operation. Pretty neat, right?
So, let's break it down, buddy. What exactly is a logarithm? Imagine you have an equation like 2 to the power of x equals 8. You probably already know that x is 3, because 2 * 2 * 2 = 8. Easy peasy, lemon squeezy! But what if the equation was 2 to the power of x equals 7? Uh oh, now it's not so straightforward, is it? That's where our superhero, the logarithm, swoops in to save the day.
A logarithm basically asks the question: "To what power do I need to raise this base number to get this other number?" So, for our 2x = 8 example, the logarithm would be asking, "To what power do I raise 2 to get 8?" And the answer, as we know, is 3. We write this mathematically as log base 2 of 8 equals 3. See? It’s just a fancy way of saying the same thing. It's like translating from one math language to another.
Let's get a little more formal, just for a sec. The general form is logb(a) = c. This is the same as saying bc = a. So, the 'b' is our base, the 'a' is the argument (or the number we're trying to get to), and 'c' is the exponent (or the answer to our logarithmic question). It's a little triangle of numbers, and they all relate to each other. Super interconnected, like a social media network for numbers!
Now, you'll often see two special kinds of logarithms pop up. First, there's the common logarithm. This one has a base of 10. When you see "log" without a little number next to it, it's usually implied that the base is 10. So, log(100) means log10(100). And what power do you raise 10 to to get 100? That's right, it's 2! Because 102 = 100. Mind. Blown. (Okay, maybe not mind-blown, but you get the idea!).

Then, we have the natural logarithm. This one is a bit more of a rebel. Its base is a special number called 'e'. You might have seen 'e' lurking around in calculus or other advanced math topics. It's approximately 2.71828. Don't ask me why it's that number, it just is. It's like the Pi of exponential functions. When you see "ln" instead of "log," that's your signal for the natural logarithm. So, ln(e5) would be 5, because, again, it's asking "to what power do I raise 'e' to get e5?" The answer, obviously, is 5. It's like the logarithm is saying, "Yep, you got this!"
Okay, so why are these things even useful? Great question! Logarithms are used all over the place. Think about measuring the intensity of earthquakes (that's the Richter scale – a logarithmic scale, by the way!), or figuring out how loud a sound is (decibels are logarithmic too!). They're also super handy in science for modeling things like population growth or radioactive decay. They help us deal with numbers that get really big or really small in a more manageable way. It's like having a cosmic shrink ray for numbers!
Now, let's talk about those homework answers, because I know that's what you're really here for, right? 😉 The key to conquering those problems is understanding the definition of a logarithm and how it relates to exponential form. If you're stuck on a problem that looks like log3(x) = 2, you just need to rewrite it in exponential form. That would be 32 = x. And boom, x = 9! See? You're already a logarithm ninja.

What about solving equations? Sometimes you'll have equations where the variable is in the exponent, like 5x = 125. Before logarithms, this was tricky. But now? We can take the logarithm of both sides. It’s like a secret weapon. You could take the common log (base 10) of both sides: log(5x) = log(125). And here's a cool property: you can bring that 'x' down in front! So, it becomes x * log(5) = log(125). Then, you can just divide both sides by log(5) to get x by itself. x = log(125) / log(5). You might need a calculator for the actual number, but you’ve isolated the variable! It’s like playing algebraic chess.
Another common type of problem will involve properties of logarithms. These are your best friends when you're simplifying expressions. There are three main ones to remember: the product rule, the quotient rule, and the power rule. Get these down, and you'll be unstoppable. Seriously, unstoppable.
The product rule says that logb(mn) = logb(m) + logb(n). Think of it as "logs of products are sums of logs." So, if you have log(6), you can rewrite it as log(2 * 3), which then becomes log(2) + log(3). It's like breaking down a big task into smaller, more manageable ones. Very efficient, very math-y.
The quotient rule is the flip side: logb(m/n) = logb(m) - logb(n). This one is "logs of quotients are differences of logs." So, log(5/2) is the same as log(5) - log(2). It’s like saying, "If I divide, I subtract my logs." Simple as that.

And the power rule, which we kind of saw earlier, is logb(mp) = p * logb(m). This is the one that lets you wrestle those exponents down. If you have log(x3), you can turn it into 3 * log(x). This is huge for solving equations and simplifying things. It's like giving the exponent a little nudge and telling it to come down and play.
Sometimes, homework problems will ask you to condense logarithmic expressions. This means taking an expression with multiple logarithms and squishing it back into a single logarithm. You'll use those three rules in reverse. For example, if you see 2log(x) + log(y), you first use the power rule backwards on the 2log(x) to get log(x2). Then, you have log(x2) + log(y). Now, use the product rule in reverse, and bam! You have log(x2 * y). See? It's like a puzzle, and you're putting the pieces back together.
Other problems might ask you to expand logarithmic expressions. This is just the opposite – taking a single logarithm and breaking it down into more parts. So, if you have log( (x2 * y) / z3 ), you'd use the rules to expand it. First, the quotient rule: log(x2 * y) - log(z3). Then, use the product rule on the first part: log(x2) + log(y) - log(z3). Finally, use the power rule on the terms with exponents: 2log(x) + log(y) - 3log(z). Poof! Expanded. It's like taking a complicated LEGO structure and showing all the individual bricks.

Don't forget about change of base. Sometimes you'll have a logarithm with a base that your calculator doesn't directly understand, like log7(49). Most calculators only have buttons for common logs (base 10) and natural logs (base e). The change of base formula to the rescue! It says logb(a) = logc(a) / logc(b). So, to calculate log7(49), you can use your calculator as log(49) / log(7) or ln(49) / ln(7). Both will give you the answer, which, in this case, is 2 (since 72 = 49). It’s like having a universal translator for logarithms.
When you’re working through your Common Core Algebra 2 homework answers, really focus on these core concepts: what a logarithm is, how to convert between exponential and logarithmic form, and how to use those three essential properties (product, quotient, power). Once you’ve got those down pat, the rest will start to fall into place. It’s like learning your ABCs before you can write a novel.
And if you're staring at a problem and your brain just freezes, take a step back. Ask yourself: "What is this problem really asking me?" Is it asking me to solve for an exponent? Is it asking me to simplify? Is it asking me to expand? Once you can identify the goal, it's much easier to figure out the steps. Don't be afraid to jot down the definitions and properties on a scratch piece of paper. We’re all about making our lives easier here, right?
Remember, math isn't about memorizing a bunch of random rules. It's about understanding how things connect. Logarithms are a beautiful example of how different mathematical ideas can be linked together. They're the bridge between exponents and a whole world of cool applications. So, next time you see that "log" symbol, don't panic. Just remember what it's asking, and you'll be well on your way to conquering those homework answers. You’ve got this!
