Introduction To Geometry Points Lines And Planes Worksheet Answers
Hey there, fellow earthlings and armchair mathematicians! Ever found yourself staring at a pizza and thinking, "Wow, this is a perfect circle... but is it really a perfect circle? Or just a very, very good approximation?" Well, guess what? You've already dipped your toes into the fascinating world of geometry. It's not just about stuffy textbooks and confusing theorems; it's about understanding the very fabric of the world around you, from the crumbs on your toast to the vastness of the cosmos. And today, we're going to take a super chill dive into the absolute basics: points, lines, and planes. Think of it as geometry's "hello, world" moment.
Now, I know what some of you might be thinking. "Geometry? Isn't that the subject where they make you draw triangles until your fingers cramp?" And yeah, sometimes it feels like that. But at its heart, geometry is just a way of describing space and the shapes within it. It's like learning the alphabet before you can write a novel. And today, we’re tackling the ABCs: the point, the line, and the plane.
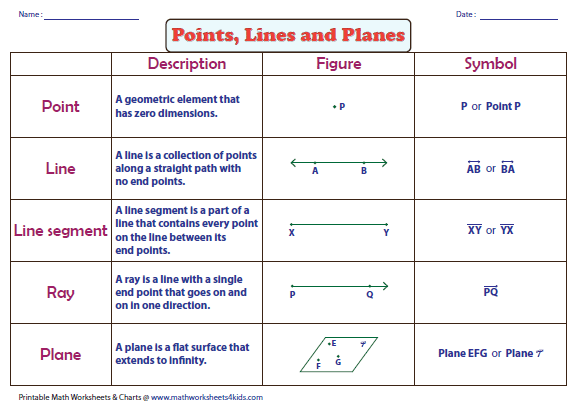
Let's kick things off with the humble, yet mighty, point. What is a point? In geometry, it's basically the smallest, most insignificant dot you can imagine. It has no size, no length, no width, and no depth. It's like that one single grain of salt that insists on escaping the shaker and landing exactly where you don't want it. Purely theoretical, but oh-so-fundamental. In your worksheet, you might see it represented by a tiny dot and labeled with a capital letter, like 'A' or 'B'. It's like giving a name to absolutely nothing. A bit like naming a pet rock – it’s a placeholder for something that doesn't really have anything else.
Think about it: when you're trying to tell someone where to meet you, you might say, "Meet me at the corner of Elm and Main." That corner, in a perfect world, is a point. It's that precise spot. Of course, in the real world, corners are usually a bit fuzzy, maybe a bit worn down from all the foot traffic. But in geometry, we can imagine the ideal corner, the one that exists only in our minds (and on our worksheets). It’s that infinitesimally small location where two streets would cross if they were perfectly straight and met at a perfect angle. Weirdly specific, right?
Next up, we have the line. Now, a line is like the point's much more adventurous cousin. A line is a straight path that goes on forever in both directions. Imagine a super-long piece of spaghetti that you could stretch out in one direction, and then keep stretching it, and stretching it, and it would never end. And then, imagine doing the same thing in the opposite direction. That's a line! It has length, but it has no width or thickness. It's like the universe's most dedicated one-dimensional highway. No exits, no rest stops, just endless straightness.
On your worksheet, a line will usually be drawn with a straight stroke and have little arrows on both ends. Those arrows are super important – they're geometry's way of screaming, "This thing keeps going and going and going!" You can name a line by picking two points on it and using those letters, like line AB. Or, if you're feeling fancy, it might have a single lowercase letter name, like line 'l'. It’s like having a street name versus naming it after the two intersections it connects. Same endless highway, different nickname.
Ever tried to draw a perfectly straight line without a ruler? It's a challenge, right? You get a bit wobbly, maybe a bit zig-zaggy. That's because our hands aren't perfect tools. But a geometric line? It's always perfectly straight. It's the Platonic ideal of straightness. Think about the laser beam from a sci-fi movie. That's a pretty good visual for a geometric line, assuming it never runs out of laser juice.

Now, lines get together and do interesting things. When two lines meet, they can form angles. You know, like the sharp corner of a slice of pizza, or the way your elbow bends. Those are angles. And the point where they meet? That's called a vertex. It's like the pointy bit of a party hat.
But what if you have lots of lines? Or what if a line just decides it doesn't want to be confined to just two directions? That's where we bring in the plane. A plane is like a perfectly flat surface that extends forever in all directions. Imagine the most perfectly flat table you've ever seen, but then imagine it stretching out infinitely in every direction. No bumps, no curves, just pure, unadulterated flatness. It's like the surface of a calm lake on a windless day, but that lake goes on forever.
On your worksheet, a plane is often represented by a tilted rectangle or a parallelogram. That's just a visual trick to give it a sense of depth and show that it's a flat surface. Think of it like drawing a 3D box on a 2D piece of paper – it’s a representation, not the real deal. The arrows on the sides of the representation? They mean it keeps going forever in those directions too. So, no matter how big your piece of paper is, it can never truly contain a geometric plane. It’s like trying to catch smoke in your hand – you can sort of feel it, but you can’t hold onto it forever.
Think about the floor you're standing on. In geometry, if that floor extended infinitely in all directions and was perfectly flat, it would be a plane. Or the surface of a perfectly still pond. Or even the wall of your room, if it went on forever. All these are examples of planes. They have length and width, but no thickness. It's like the ultimate, super-thin, infinitely large sheet of paper.

So, why do we care about these abstract concepts? Because they are the building blocks for everything else in geometry. You can't have a triangle without lines. You can't have a square without lines. You can't even have a 3D object like a cube without thinking about the planes that form its surfaces. It's all interconnected, like a giant, cosmic game of LEGO.
Let's look at some common scenarios in your "Introduction to Geometry: Points, Lines, and Planes Worksheet." You'll probably see questions asking you to identify these things in diagrams. For example, you might see a drawing of a cube. The corners of that cube? Those are your points. The edges of the cube? Those are like segments of lines (segments are just parts of lines that have a start and an end, like a piece of string that you can cut). And the flat faces of the cube? Those are representations of planes.
Sometimes, the worksheet might ask you to draw things. "Draw a line that passes through points P and Q." Easy peasy. Just imagine a super-straight, endless path connecting those two little dots. Or, "Draw a plane and label a point R on it." Again, just a flat, endless surface with a tiny dot somewhere on it. It's like doodling, but with a purpose!
Another common task is identifying collinear and coplanar points. Collinear just means points that lie on the same line. Imagine people sitting on a very, very long, straight bench. They are collinear. If you've got a few points on your worksheet that are all in a row, they’re collinear. It’s like a straight train of thought.
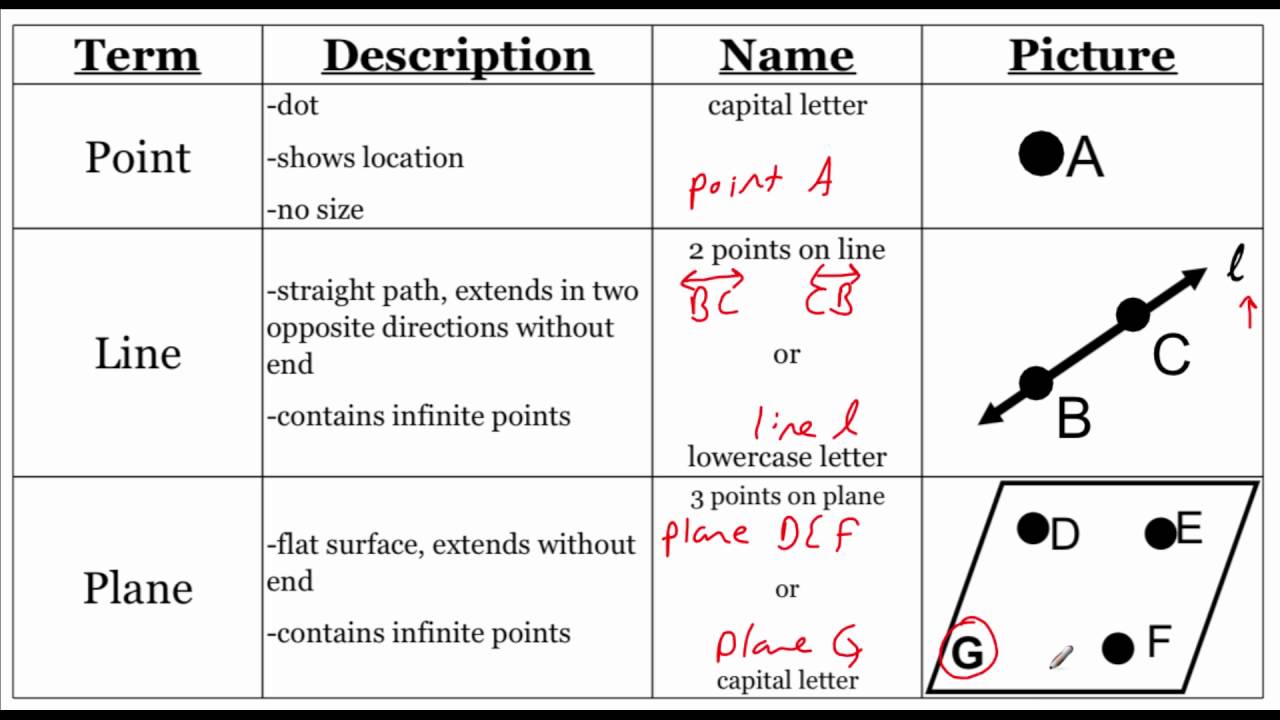
Coplanar means points that lie on the same plane. Imagine a bunch of stickers stuck on a single, flat wall. They are coplanar. If you have a bunch of points scattered across the surface of that tilted rectangle on your worksheet, and they all belong to that same flat, endless surface, they are coplanar. It’s like a group of friends all chilling on the same perfectly flat beach blanket.
What if some points are on the same line, but others aren't? Then they're not all collinear, but they might still be coplanar. It's like having some friends on the beach blanket sitting in a straight line, and others just scattered around. They're all on the same blanket (coplanar), but not everyone is sitting on the same straight path (collinear).
You might also encounter the concept of non-collinear points. These are points that don't all lie on the same straight line. Imagine three friends trying to walk in a straight line, but one of them keeps veering off to look at butterflies. Those three friends are non-collinear. They can't all fit on the same single, endless straight path.
And when it comes to planes, you might hear about non-coplanar points. These are points that cannot all lie on the same single, flat plane. Imagine you have a few points on your desk (that's a plane). But then you have a point floating in the air above your desk, and another point below your desk. Those points are non-coplanar because you can't lay a single, flat, endless surface over all of them simultaneously. It's like trying to balance a book on three points on a table, and then trying to balance another book on three points, one of which is way up in the air. You can't do it with just one flat surface.

Your worksheet answers will be the results of you applying these basic ideas. If the question is "Identify the points in the diagram," you'll just list the letters that are labeling the dots. If it's "Draw a line segment," you'll draw a straight line with two endpoints. If it's "Are points X, Y, and Z collinear?" you'll look at your drawing and see if they all fit on one straight line. If they do, the answer is "Yes." If they don't, it's "No."
Think of it like this: imagine you're a detective and your worksheet is your crime scene. The points are the clues, the lines are the possible paths the suspect took, and the planes are the rooms they could have been in. Your job is to figure out how these elements relate to each other based on the evidence presented.
Don't sweat it if it feels a little abstract at first. Geometry is like learning a new language, and these are the very first words. The more you practice, the more comfortable you'll become. Soon, you'll be looking at the world around you and seeing points, lines, and planes everywhere. You'll see the intersection of two streets as a point, the horizon as a line (or at least a segment of one!), and a flat wall as a plane.
So, grab your pencil, embrace the dots and dashes, and remember that even the most complicated geometric proofs start with the simple elegance of a point, a line, and a plane. They're the fundamental building blocks of space, and understanding them is your first step into a much bigger, much cooler world. Happy doodling!
