In A Perfectly Elastic Collision Between Two Perfectly Rigid Objects
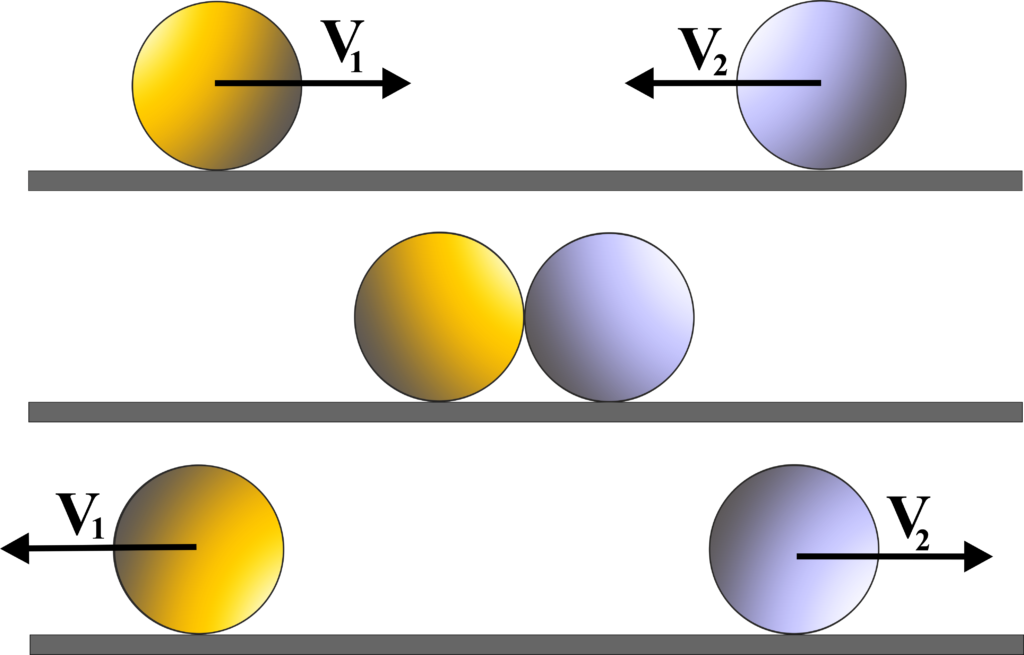
Ever wondered what happens when two super-tough, perfectly bouncy balls smack into each other? It sounds like something out of a cartoon, right? But believe it or not, this seemingly simple scenario is a cornerstone of physics and has some seriously cool implications that touch our everyday lives. We're talking about a perfectly elastic collision, a concept that might sound a bit technical, but at its heart, it's all about understanding how things move and interact without any wasted energy.
Think about it: when you play billiards, the way the cue ball sends other balls flying is a fantastic, real-world (almost!) example of this idea. Or imagine tiny particles zipping around in a gas. They bump into each other constantly, and understanding these collisions is key to figuring out how gases behave. It's not just about hitting things; it's about predicting motion, energy transfer, and the fundamental rules that govern the universe. The beauty of a perfectly elastic collision is its purity. In this idealized world, nothing gets lost. No heat, no sound, no deformation – just a clean exchange of momentum and energy. It’s like a perfect dance where every step is precisely mirrored by the other dancer, with no awkward stumbles or lost rhythm.
The Magic of No Waste
So, what's the big deal about a "perfectly elastic collision between two perfectly rigid objects"? The 'perfectly rigid' part means that when these objects collide, they don't bend, squash, or change shape at all. Imagine two indestructible billiard balls made of diamond. And 'perfectly elastic' means that when they bounce off each other, they don't lose any energy. No energy is turned into heat, sound, or permanent dents. It’s like they have a magical, invisible spring connecting them that simply pushes them apart with all the energy they had right before the impact.
The primary purpose and immense benefit of studying this concept lies in its ability to provide a foundational model for understanding interactions. In the real world, perfectly elastic collisions are rare. Most collisions involve some energy loss. However, by first understanding the "ideal" scenario, physicists can then more accurately analyze and predict the behavior of real-world systems by accounting for these energy losses. It’s like learning the basic rules of a game before you start adding in all the special moves and power-ups. This idealization helps us build accurate mathematical models that can be applied to a vast range of phenomena.
Consider the implications: in the realm of atomic and subatomic physics, collisions between particles are often approximated as perfectly elastic. This understanding is crucial for fields like nuclear physics and particle accelerators, where precise energy and momentum transfers are paramount. Imagine designing an experiment to create new particles; you need to know exactly how much energy your colliding particles will have and how that energy will be distributed after the collision. Without the framework of elastic collisions, this would be an impossible task. It allows scientists to 'see' and understand the invisible world by observing how these tiny entities bounce off each other.
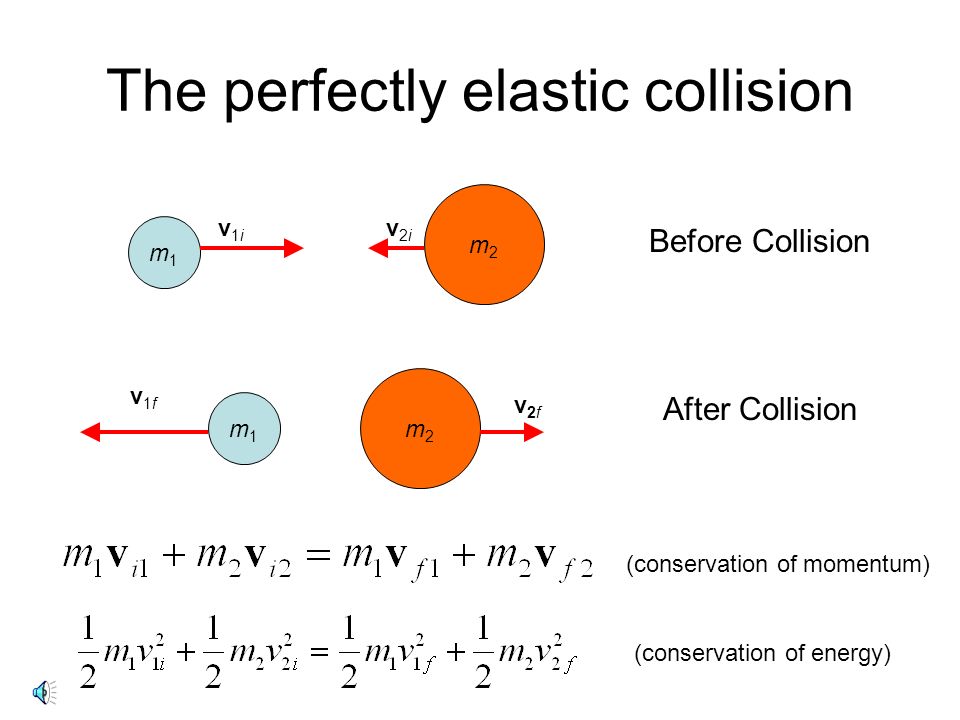
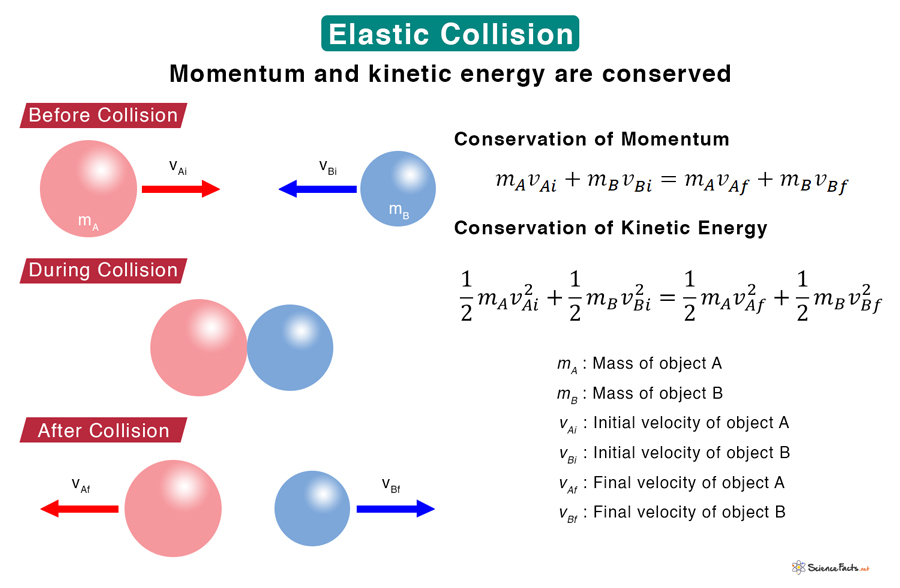
"In a perfectly elastic collision, the total kinetic energy of the system is conserved."
This conservation of kinetic energy is the key differentiator. Kinetic energy, the energy of motion, remains exactly the same before and after the collision. This is a powerful concept because it simplifies many calculations. Instead of having to track energy lost to heat or deformation, we know that whatever energy the objects had combined right before they touched, they will have that same amount combined right after they separate. It’s a closed loop of motion, a perfect transfer of ‘oomph’.
Beyond the Bouncy Balls
But the benefits extend far beyond the microscopic. Think about engineering. When engineers design safety features for vehicles, like crumple zones, they are implicitly dealing with inelastic collisions. However, understanding the principles of elastic collisions provides a crucial baseline for analyzing impact forces and energy absorption. By knowing what happens in an ideal scenario, they can better design materials and structures that dissipate energy effectively in a crash, protecting occupants.
Even in something as seemingly simple as designing a new type of athletic equipment, like a tennis racket or a golf club, the physics of collisions comes into play. The way the ball bounces off the racket or club face is governed by these principles. A more elastic collision might mean a faster ball speed, while a less elastic one might mean less power. The ideal elastic collision serves as a benchmark for optimizing performance.
Furthermore, the concept of perfectly elastic collisions is fundamental to understanding thermodynamics. For example, the kinetic theory of gases, which explains the macroscopic properties of gases (like pressure and temperature) based on the motion of their constituent molecules, relies heavily on the assumption that collisions between gas molecules are perfectly elastic. This assumption allows for the derivation of fundamental gas laws and the understanding of concepts like temperature as a measure of average kinetic energy. Without this simplification, the mathematical models describing gas behavior would be overwhelmingly complex.
So, the next time you see a perfectly clear bounce, whether it’s a basketball hitting the pavement or a science demonstration, remember the elegant simplicity and profound importance of a perfectly elastic collision. It’s a concept that, while idealized, provides an indispensable lens through which we understand the dynamic and energetic nature of our universe, from the smallest particles to the grandest cosmic events. It’s a testament to how abstract physics can provide practical insights into the world around us.
