How To Find Midpoint Of A Line (step-by-step Guide)
Let's talk about something that sounds a little bit mathy but is actually super handy and, dare I say, fun to know: finding the midpoint of a line. Think of it like finding the exact center point between two spots. It’s like a little discovery, a neat little trick that can make things easier in all sorts of ways. Whether you're doodling on graph paper, planning out a project, or even just trying to understand a cool concept, knowing how to find this middle ground is a valuable skill.
So, why bother learning this? For beginners, it’s a gentle introduction to coordinate geometry, showing how numbers can represent shapes and positions. It’s like learning your first magic spell in the world of math! Families can use it for fun activities, like plotting treasure map points on a grid and finding the halfway spot to the treasure. Imagine a scavenger hunt where the next clue is exactly in the middle of two marked locations! Hobbyists, like those who enjoy model building or digital art, might find it useful for ensuring symmetry or finding the exact center of a design element. Even if you’re just curious, it’s a satisfying little puzzle to solve.
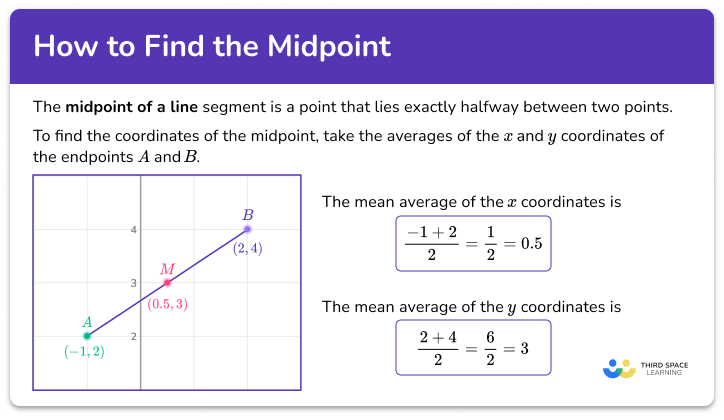
Let's get to the step-by-step guide. Imagine you have two points on a graph. Each point has an 'x' coordinate and a 'y' coordinate. Let's call our first point (x1, y1) and our second point (x2, y2). To find the midpoint, you just need to do two simple calculations:
Step 1: Find the middle of the x-coordinates. You do this by adding the two x-values together and dividing by 2. So, the midpoint's x-coordinate will be (x1 + x2) / 2.
Step 2: Find the middle of the y-coordinates. Do the exact same thing with the y-values. Add the two y-values together and divide by 2. The midpoint's y-coordinate will be (y1 + y2) / 2.

And voilà! Your midpoint is the new point you just calculated: ((x1 + x2) / 2, (y1 + y2) / 2). It's that simple!
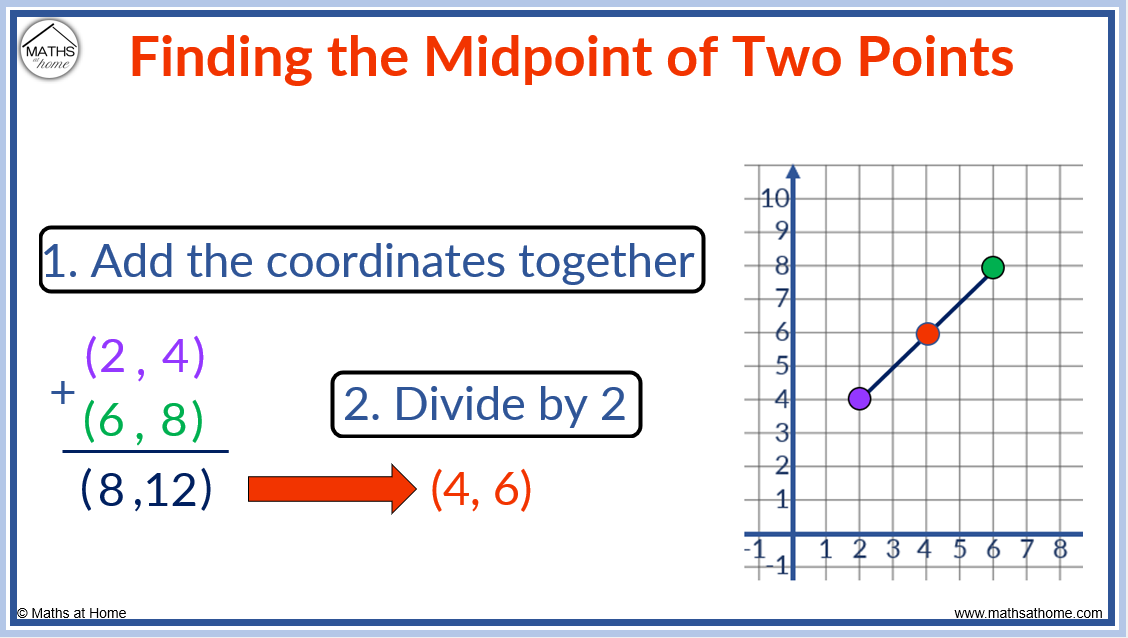
Let's try an example. Suppose you have a point at (2, 4) and another at (8, 10). To find the midpoint:
Midpoint x = (2 + 8) / 2 = 10 / 2 = 5

Midpoint y = (4 + 10) / 2 = 14 / 2 = 7
So, the midpoint of the line between (2, 4) and (8, 10) is (5, 7). See? Not so scary after all!
A fun variation is thinking about this in the real world. If you have two friends standing at different points in a park, the midpoint is the perfect spot for them to meet if they want to travel the same distance to get there. Or, if you're laying out a garden path between two points, finding the midpoint can help you center other features.
For getting started, grab some graph paper and a pencil. Plot a few points, connect them with a line, and then use the formula to find the midpoint. You can even try drawing a triangle and finding the midpoint of each side. It’s a fantastic way to practice and build your confidence. The more you play around with it, the more natural it becomes.
In conclusion, finding the midpoint of a line is a clever little mathematical tool that opens up possibilities for problem-solving, creative projects, and even just for the pure satisfaction of understanding how things work. It’s a small piece of knowledge that offers a surprising amount of utility and, best of all, it’s easy to learn and enjoyable to use.
