Graphing A Piecewise-defined Function Problem Type 1 Aleks Answers
Hey there, math adventurers! Ready to dive into the wonderful world of piecewise-defined functions? Don't worry, it's not as scary as it sounds. Think of it like a choose-your-own-adventure story, but with graphs! And guess what? We're going to tackle a specific type of problem that pops up a lot, especially when you're learning on platforms like ALEKS. We're talking about "Graphing a Piecewise-Defined Function Problem Type 1." Sounds official, right? But really, it's just about piecing together different graph segments to make one complete picture.
So, what exactly is a piecewise-defined function? Imagine a function that has different "rules" for different "sections" of its domain. It’s like having a magic coat that changes its style depending on the weather. If it's sunny, it's a cool t-shirt. If it's rainy, it's a waterproof jacket. And if it's snowing? Bam! A cozy parka. Each piece of the function is like one of those weather-appropriate outfits, and together, they make up the whole function's personality. Pretty neat, huh?
Now, when we talk about "Problem Type 1" on ALEKS, it usually means we're dealing with the simplest kind of piecewise functions. We're typically looking at functions made up of straight lines. Yep, just good old straight lines. No crazy curves or squiggles to make your head spin. This is where we build our foundation, so let's get comfortable with these linear pieces.
So, how do we actually graph these things? The key is to break it down. A piecewise function will usually be presented something like this:
f(x) = { ... some linear equation ... if x < some number
{ ... another linear equation ... if some number <= x < some other number
{ ... yet another linear equation ... if x >= some other number
See those "if" statements? Those are your dividers. They tell you where one piece of the graph ends and the next one begins. It's like road signs on your graphing journey, pointing you in the right direction.
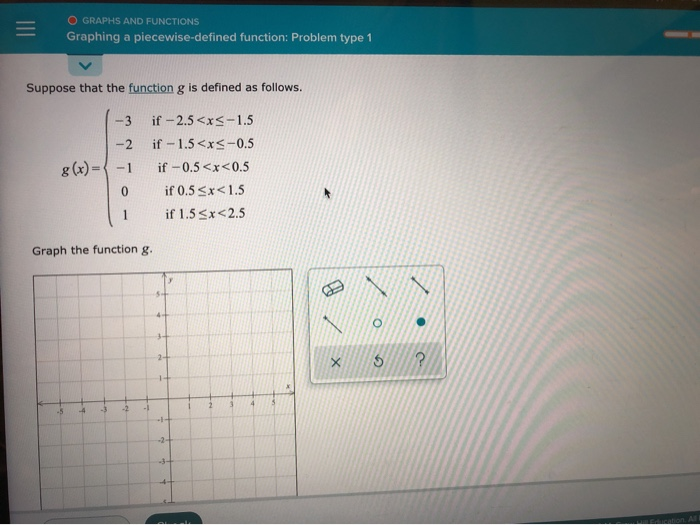
Let's say we have a function like this:
f(x) = { 2x + 1 if x < 2
{ -x + 5 if x >= 2
Our job is to graph this. First, we look at the domain. We've got two "pieces" to worry about: one for everything less than 2, and one for everything greater than or equal to 2. These are our two worlds, and we need to draw the correct function in each world.
Let's tackle the first piece: f(x) = 2x + 1 if x < 2. This is a standard linear equation, y = 2x + 1. If it were for all x values, we'd just graph it as a line. But here, it only applies when x is less than 2. So, we need to find out what's happening at and around x = 2.
When x = 2, the expression 2x + 1 would give us 2(2) + 1 = 5. But since our condition is x < 2 (strictly less than 2), this point (2, 5) isn't actually on our graph for this piece. It's like an imaginary friend who's always there, but you can't quite touch them. This means we'll use an open circle at (2, 5) to show that this point is excluded from this part of the function.
Now, to draw the rest of the line, we need at least one more point. Let's pick an x-value that's definitely less than 2, say x = 0. If x = 0, then y = 2(0) + 1 = 1. So, we have another point at (0, 1). Since this is a straight line, we can connect our imaginary point at (2, 5) with our real point at (0, 1) and draw a line segment that goes to the left from (0, 1) and extends all the way to the open circle at (2, 5).
This line segment represents the first part of our piecewise function. It's a happy little line happily cruising along, but it stops (with a little warning sign!) right before it hits x = 2.
Okay, ready for the second piece? This one is f(x) = -x + 5 if x >= 2. Again, this is a linear equation, y = -x + 5. This time, it applies when x is greater than or equal to 2. This is where our other world begins.
Let's check the boundary point again, x = 2. This time, our condition is x >= 2, which means x = 2 is included. So, when x = 2, y = -(2) + 5 = 3. This point (2, 3) is definitely part of our graph for this piece, so we'll mark it with a closed circle.
Now we need another point for this line. Let's pick an x-value greater than 2, say x = 4. If x = 4, then y = -(4) + 5 = 1. So, we have another point at (4, 1).
We can now connect our closed circle at (2, 3) with our point at (4, 1) and draw a line segment extending to the right from (2, 3). This segment shows the behavior of the function for all x-values greater than or equal to 2.
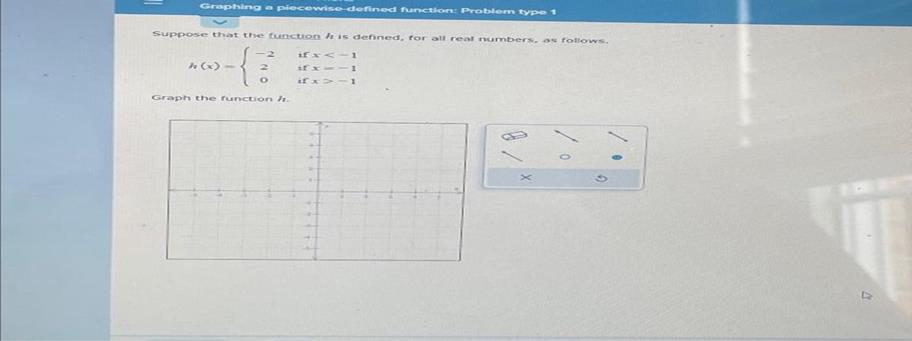
And voila! You've just graphed a piecewise-defined function! You have two distinct line segments, each obeying its own rule, and they meet (or almost meet!) at the dividing point. It's like two puzzle pieces that fit together perfectly to create a beautiful picture.
The key things to remember for this "Problem Type 1" are:
- Identify the pieces: Look at the different equations and their corresponding domain restrictions.
- Find the boundary points: These are the x-values where the "rules" change.
- Determine open vs. closed circles: Use an open circle (o) for strict inequalities (<, >) and a closed circle (•) for inclusive inequalities (<=, >=). This is super important!
- Calculate points: For each piece, pick at least two points. One should ideally be the boundary point (to determine the circle type and value) and another point within the domain restriction to get the direction of the line.
- Draw the segments: Connect your points with straight lines, making sure they extend in the correct direction (left for x < a, right for x > a, both ways if it were a different type of function, but not for Type 1).
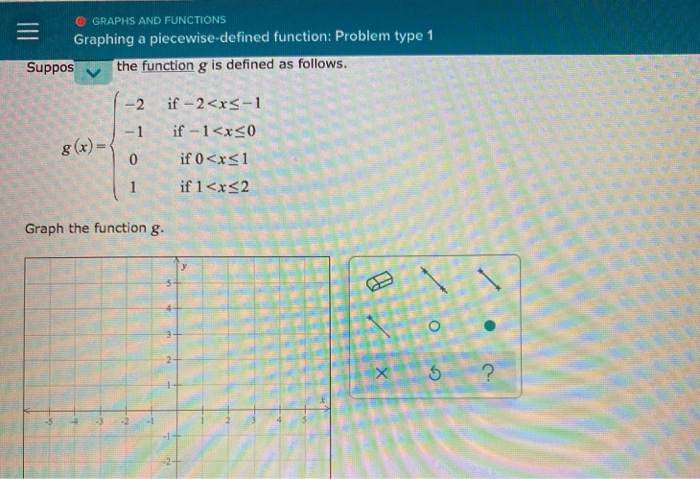
Sometimes, the piecewise functions can have more than two pieces. For example:
g(x) = { x - 1 if x < 0
{ 2 if 0 <= x < 3
{ -x + 5 if x >= 3
In this case, you have three worlds to graph in! You'd follow the same process for each piece. The first piece is a line for x < 0. The second piece is a horizontal line at y = 2 for x between 0 and 3 (including 0 but not 3). And the third piece is another line for x >= 3. You'd have two boundary points to consider: x = 0 and x = 3.
At x = 0, the first piece (x - 1) would be 0 - 1 = -1. Since it's x < 0, you'd have an open circle at (0, -1). The second piece (y = 2) starts at x = 0 and is included, so you'd have a closed circle at (0, 2). Notice how the graph "jumps" at x = 0! That's perfectly fine for piecewise functions. They don't have to be continuous (meaning they don't have to be drawn without lifting your pencil).
At x = 3, the second piece (y = 2) ends because it's x < 3. So, you'd have an open circle at (3, 2) for this piece. The third piece (-x + 5) starts at x = 3 and is included (x >= 3). So, you'd have a closed circle at -(3) + 5 = 2, which is (3, 2). Hey, look at that! The open circle from the left and the closed circle from the right meet at the same point. This means this graph is continuous at x = 3. That’s a bonus!
It might seem a bit fiddly at first, but with a little practice, you'll get the hang of it. ALEKS is great because it gives you the tools to click and drag points, draw lines, and place circles. So, embrace the interactive nature of it!
Don't get discouraged if your first few attempts aren't perfect. Math is all about learning from your mistakes. Think of each graph as a practice sketch. The more you draw, the better you'll become. You’re building a valuable skill, and understanding these functions is a stepping stone to more complex mathematical concepts. Plus, imagine being able to tell people you can "graph piecewise functions"! Sounds pretty smart, right?
So, next time you see a piecewise function problem, take a deep breath, put on your graphing hat, and remember these steps. You've got this! You're not just solving math problems; you're becoming a master of breaking down complexity and building clear, beautiful representations. Keep practicing, keep experimenting, and most importantly, keep that amazing brain of yours engaged. You're doing fantastic, and every graph you draw is a step closer to mathematical mastery and a big, happy smile!
