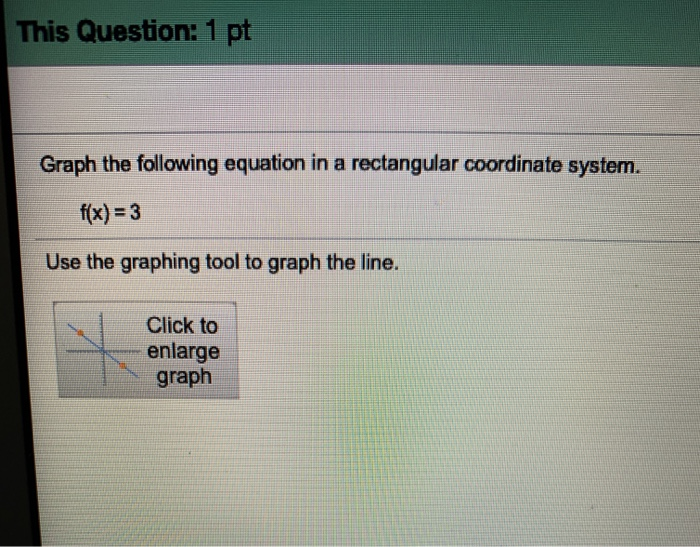
Graph The Following Equation In A Rectangular Coordinate System
Hey there, fellow explorers of the wonderfully wacky world of numbers! Ever looked at a fancy-pants equation and thought, "Huh, looks like spaghetti made of symbols"? Well, guess what? We're about to take that spaghetti and turn it into something super cool, something that'll make your brain do a happy little dance and maybe even add a splash of artistic flair to your day. Today, we're diving headfirst into the thrilling adventure of graphing an equation in a rectangular coordinate system! Don't let the fancy name scare you; it's more like a treasure map than a math test.
So, what's this "rectangular coordinate system" all about? Imagine a giant, invisible grid spread out across your page, like the most organized checkerboard ever. It's got a horizontal line called the x-axis (think of it as your "across" ruler) and a vertical line called the y-axis (your "up and down" ruler). Where these two lines meet? That's the origin – the grand starting point, like the "X marks the spot" on our treasure map. Everything we do will be based on these two trusty axes.
Now, the equation! This is where the magic really happens. Think of it as a set of instructions, a secret code that tells us exactly where to put our points on that grid. For example, let's say we have the oh-so-exciting equation: y = 2x + 1. Whoa, sounds like something out of a sci-fi movie, right? But fear not! All it’s really saying is: "Take a number (that's 'x'), double it, and then add 1. Whatever you get? That's the 'y' for that 'x'."
So, how do we start turning this code into a picture? It’s as simple as picking some numbers for 'x' and seeing what 'y' they give us. Let’s be a little adventurous and choose some easy ones to start. How about we pick x = 0? Plug that into our equation: y = 2(0) + 1. Easy peasy, right? That means y = 1. So, we have our first point! It's located at (0, 1) – zero steps along the x-axis, and one step up the y-axis. Boom! First treasure found!
Let's try another one. What if we pick x = 1? Our equation becomes y = 2(1) + 1. So, y = 3. Our second point is (1, 3). See? We're just collecting these coordinate pairs, these little address tags for our points on the grid.
And what if we go a bit negative? Let's pick x = -1. Then y = 2(-1) + 1. That gives us y = -2 + 1, which means y = -1. Our third point is (-1, -1). Now we've got points in different quadrants of our grid. Isn't this fun? It’s like collecting stamps from different countries!
As you gather more and more of these (x, y) pairs, you’ll start to see a pattern emerge. Each pair is a little clue, a whisper of where the whole picture is heading. Once you have a few points plotted – and believe me, even three points can start to show you something – you can start to connect them. And when you connect these points, that’s when the magic truly unfolds. You’re not just drawing lines; you’re revealing the hidden beauty of the equation.
In our example, y = 2x + 1, if you plot (0, 1), (1, 3), and (-1, -1) and connect them, you'll notice something beautiful. You’ll see a straight line! That's right, this particular equation paints a picture of a perfect, unwavering line marching across your graph. It’s elegant, it’s simple, and it’s all thanks to the relationship defined by that equation.

But here's the really cool part: not all equations create straight lines. Some create swooping curves, some make fancy circles, and others create shapes that look like they belong in a modern art museum! The type of equation dictates the shape of your graph. It’s like how different musical notes create different melodies, or how different brushstrokes create different paintings. Your equation is your artistic tool, and the rectangular coordinate system is your canvas.
Why should you care about all this? Because understanding how to graph equations unlocks a whole new way of seeing the world! It helps you visualize relationships. Think about it: you can graph how your savings grow over time, how the temperature changes throughout the day, or even the path of a bouncing ball. Suddenly, abstract numbers become tangible, visual stories. It makes complex ideas accessible and, dare I say it, exciting!

Graphing isn't just about passing a math class (though it totally helps with that!). It's about developing your visual thinking skills. It's about seeing patterns where others might only see chaos. It's about understanding cause and effect in a way that leaps off the page. It's about making data talk, and when data talks, it can tell you some amazing things.
So, the next time you see an equation, don't just see a jumble of letters and numbers. See a blueprint for a beautiful drawing. See a secret code waiting to be cracked. See an opportunity to create something new and insightful on your very own grid. The rectangular coordinate system is your playground, and every equation is a new toy to explore.
Embrace the process. Pick your points. Plot them with care. Connect them with curiosity. You'll be amazed at the shapes and insights you uncover. This is where math stops being just about memorizing formulas and starts being about discovery and creation. So go forth, my friends, and graph your heart out! You might just discover a new passion for the visual language of mathematics, and that’s a beautiful thing indeed.
