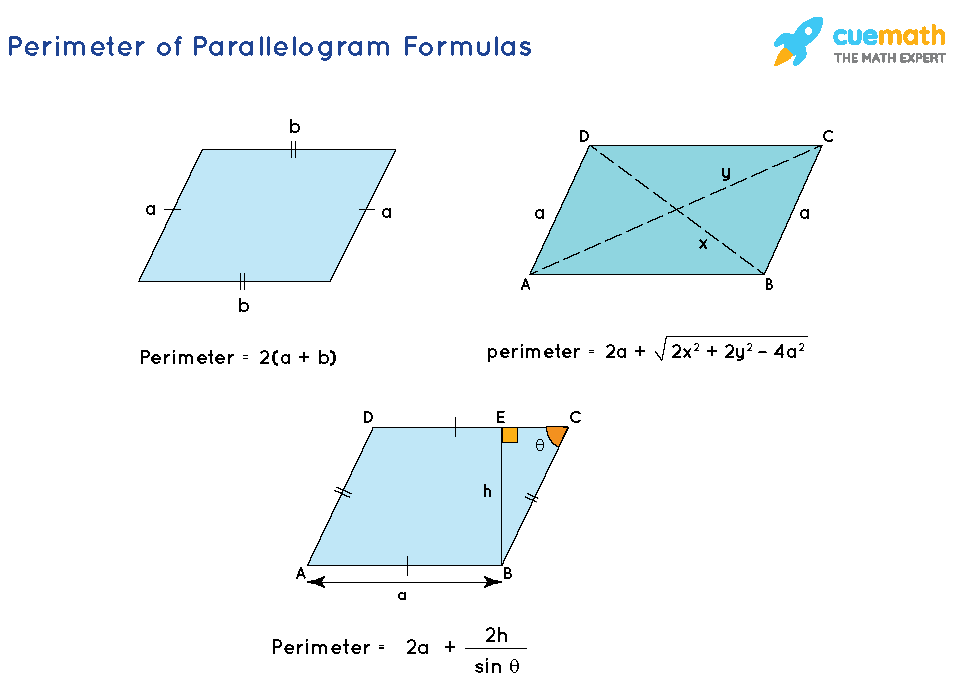
Find The Perimeter Of The Parallelogram With These Vertices
Hey there, math explorers and curious minds! Ever find yourself staring at a bunch of dots on a graph and wondering what kind of shape they're forming? Maybe you've even been asked to, you know, find the perimeter of that shape. Today, we're diving into the wonderfully chill world of parallelograms and how to figure out their sneaky, slanty boundaries. No sweat, no cramming – just a friendly chat about a cool little geometric puzzle.
So, what's a parallelogram? Think of it like a squished rectangle. You know how rectangles have those perfectly parallel sides that never meet, no matter how long you draw them? Parallelograms are the same, but they've been nudged a bit. They have two pairs of parallel sides. Imagine a deck of cards – if you push the top edge over to the side, you get a parallelogram! Or maybe a wonky doorframe? Yep, that's a parallelogram too.
And what's a perimeter, you ask? It's just the total distance around the outside of any shape. Think of it like putting a tiny fence around your garden. The length of that fence is the perimeter. For a parallelogram, it's the sum of all four of its sides. Easy peasy, right?
The Vertex Voyage: Navigating Our Parallelogram
Now, the fun part: we're given the coordinates of the corners, or vertices, of our parallelogram. These are like the secret codes that tell us exactly where each point sits on our graph. Let's say we have these four points:
A = (1, 2)
B = (5, 2)
C = (7, 5)
D = (3, 5)
So, we have our four building blocks. Our mission, should we choose to accept it (and we totally do!), is to find the distance around this shape. How do we do that? We need to find the lengths of each side.
Side Hustle: Measuring the Parallelogram's Edges
This is where a little bit of geometry magic comes in. We can use the distance formula. Remember that? It’s like a trusty sidekick that helps us measure the straight-line distance between two points on a graph. It looks a little something like this:
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Don't let the square root and the little 'x's and 'y's scare you. It’s just a fancy way of saying: find the difference in the x-coordinates, square it; find the difference in the y-coordinates, square it; add those two squared numbers together; and then take the square root of the whole thing. It’s basically the Pythagorean theorem in disguise – always a good sign!

Let's start with the side connecting points A (1, 2) and B (5, 2). So, (x₁, y₁) is (1, 2) and (x₂, y₂) is (5, 2).
The difference in x is 5 - 1 = 4.
The difference in y is 2 - 2 = 0.
So, the distance AB is √[(4)² + (0)²] = √[16 + 0] = √16 = 4.
Hey, that was pretty straightforward! Notice how the y-coordinates were the same? That means this side is perfectly horizontal, like a calm, flat lake. That's a helpful shortcut when you see that!
Now, let's look at side BC, connecting B (5, 2) and C (7, 5).
The difference in x is 7 - 5 = 2.

The difference in y is 5 - 2 = 3.
So, the distance BC is √[(2)² + (3)²] = √[4 + 9] = √13. This is our first slanty side!
Now, here's the cool thing about parallelograms. Remember those pairs of parallel sides? They're not just parallel; they're also equal in length! So, if side AB has a length of 4, then the opposite side, CD, must also have a length of 4. We could calculate it to be sure, but we know the trick!
Let's quickly check CD, connecting C (7, 5) and D (3, 5).
The difference in x is 3 - 7 = -4. (Squaring it makes it positive, so no worries about the minus sign).
The difference in y is 5 - 5 = 0.
Distance CD = √[(-4)² + (0)²] = √[16 + 0] = √16 = 4. See? Told you so!
And if side BC has a length of √13, then its opposite side, AD, must also have a length of √13. Let’s verify with points A (1, 2) and D (3, 5).
The difference in x is 3 - 1 = 2.
The difference in y is 5 - 2 = 3.
Distance AD = √[(2)² + (3)²] = √[4 + 9] = √13. Another match!
Perimeter Party: Adding It All Up!
So, our parallelogram has two sides of length 4 and two sides of length √13. To find the perimeter, we just add up all four sides:
Perimeter = Side AB + Side BC + Side CD + Side AD
Perimeter = 4 + √13 + 4 + √13

Perimeter = (4 + 4) + (√13 + √13)
Perimeter = 8 + 2√13
And there you have it! The perimeter of our parallelogram is 8 + 2√13. It’s a bit of a fancy number, with that square root in there, but it's the exact distance around our shape. If you wanted a rough idea, √13 is about 3.6, so the perimeter is roughly 8 + 2(3.6) = 8 + 7.2 = 15.2. But we mathematicians often like to keep things exact when we can!
Why Does This Even Matter?
Okay, so you might be thinking, "This is cool and all, but when will I ever need to calculate the perimeter of a parallelogram with these specific numbers?" And that's a fair question! But the principle is what's really important. This skill is like a little tool in your brain’s toolbox. You can use it for:
- Designing things: Imagine you're building a fence around a oddly shaped garden bed, or you need to calculate how much trim to buy for a sloped roof section.
- Understanding maps: Real-world shapes aren’t always perfect squares and rectangles.
- Future math adventures: This builds a foundation for more complex geometry and even physics problems.
Think of it this way: learning to find the perimeter of a parallelogram is like learning to tie your shoelaces. You might not think about it much once you've mastered it, but it’s a fundamental skill that lets you move forward with confidence. And who knows, maybe one day you'll be designing a cool, geometric-themed playground, and you'll need to know the exact length of the frame for a slide that's a bit… slanty.
So, next time you see a parallelogram, whether it's on a graph, in a building, or even just a tilted picture frame, you'll know its secret: its perimeter is just the sum of its four sides, and you have the tools to find it!
Keep exploring, keep questioning, and remember, math can be pretty awesome when you approach it with a relaxed, curious vibe. Happy calculating!
