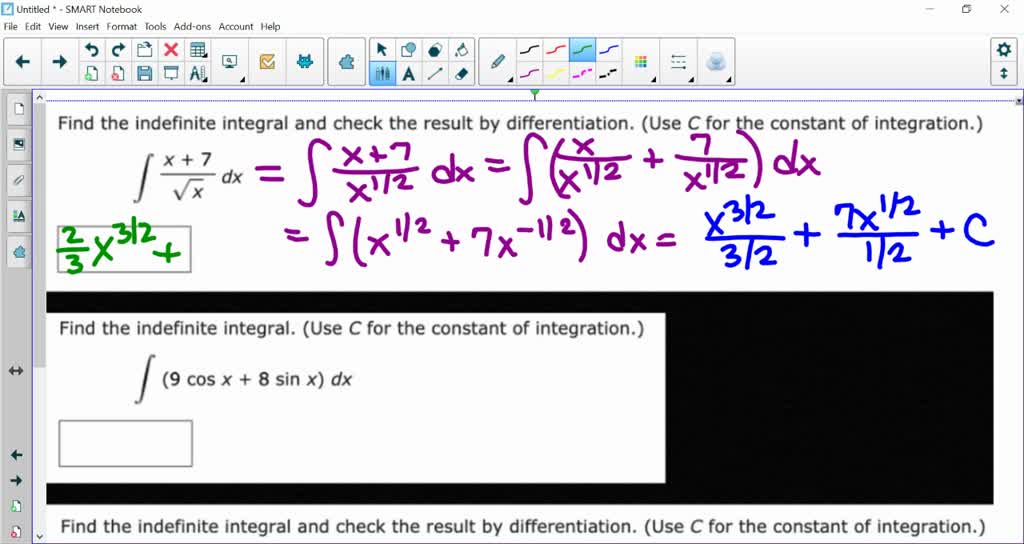
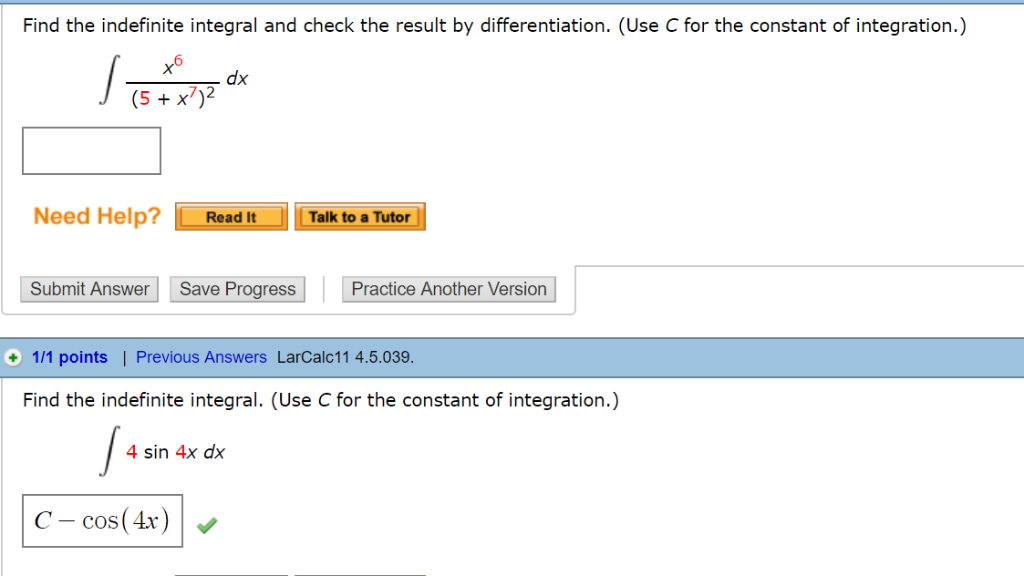
Find The Indefinite Integral And Check The Result By Differentiation

Imagine you're a detective, but instead of solving crimes, you're solving mathematical mysteries. Your mission? To find a hidden function, a secret formula that unlocks a whole family of solutions. This is the thrilling world of finding the indefinite integral!
It sounds a bit like magic, doesn't it? You're given a clue – a "derivative" – and you have to work backward to discover the original "function." It’s like seeing a shadow and trying to guess the shape that cast it. Pretty neat, huh?
And the best part? You get to play a bit of a trickster yourself. Once you think you've found your hidden function, you can prove it! How? By doing a little bit of differentiation.
This is where the fun really kicks in. You take your suspected original function and perform the opposite operation – differentiation. If your guess is right, you should end up with the exact clue you started with. It's like a mathematical "gotcha!" moment.
Think of it like this: you're trying to guess someone's secret recipe. You think you've figured out the ingredients and steps. Then, you "un-bake" it, or reverse the cooking process, to see if you get back the original raw ingredients. If you do, bingo! Your recipe is a winner.
This process, finding the indefinite integral, is also known as antidifferentiation. It’s all about going back to the source, the original. It's like tracing the path of a river back to its spring.
The indefinite integral isn't just one single function, though. That's another cool twist! When you find an indefinite integral, you always get a whole family of functions. They are all related, differing by a simple constant.
This "constant of integration" is like a secret handshake for all the functions in the family. It's represented by a lowercase 'C'. So, if F(x) is one solution, then F(x) + C represents all possible solutions.
Why is this so special? Because in many real-world problems, there isn't just one single answer. Think about a car's speed. If you know its acceleration, you can find its velocity. But the velocity could have started at different speeds. The '+ C' accounts for all those possible starting points.
So, when you're asked to find the indefinite integral, you're not just finding one answer; you're uncovering a whole universe of related functions. It's like opening a treasure chest, and instead of one gold coin, you find a whole pile!
And then comes the delightful part: checking the result by differentiation. This is your moment of triumph! You’ve put on your detective hat, followed the clues, and now you’re presenting your findings.
Let's say you've found a function you believe is the indefinite integral of another. You take your proposed answer, and you apply the rules of differentiation. If everything is correct, the derivative of your answer should perfectly match the original function you were given.
It’s like proving your magic trick. You’ve made something appear (the integral), and now you’re showing how it was done by making it disappear again (through differentiation). The audience is amazed, and you know you've got it right.
This checking process is super important. It’s not just a formality; it’s your safety net. It ensures you haven't made any slip-ups. Mathematics is all about precision, and this step guarantees that your solution is solid.
Imagine you're building something with LEGOs. You follow instructions to build a cool spaceship. Now, you want to be sure you followed them correctly. So, you carefully take it apart, brick by brick, and see if you end up with the original set of bricks. If you do, your spaceship is a masterpiece!
The act of differentiation, when used to check your integral, is like the ultimate truth serum for your mathematical work. It reveals whether your guesswork was brilliant or just a bit off.
So, you might be given a function like f(x) = 2x. Your task is to find its indefinite integral. You might guess that F(x) = x² is the answer.

Now, you need to check your result by differentiation. You take your proposed integral, F(x) = x², and differentiate it. What do you get? You get F'(x) = 2x.
Hooray! It matches the original f(x). But remember that '+ C'? The derivative of any constant is zero. So, if you had guessed F(x) = x² + 5, its derivative would also be 2x.
This is why the indefinite integral is really x² + C. The '+ C' is the placeholder for any number that could be added to x², and its derivative would still be 2x. It’s a beautiful, inclusive family!
This dance between integration and differentiation is fundamental to calculus. They are like two sides of the same coin, or perhaps even a superhero duo. One undoes what the other does, and together they unlock profound insights into how things change.
The "why" behind it all is quite fascinating. Integration helps us find areas, volumes, and accumulated changes. Differentiation helps us understand rates of change, slopes, and instantaneous velocities. They are the engines that drive much of science and engineering.

When you're solving problems, especially in physics or economics, you often deal with rates. For example, you might know how fast something is growing (its rate of change). To find out how much it has grown in total, you need to integrate.
And the beauty of checking the result by differentiation is that it’s always available to you. It’s like having a built-in error checker for your mathematical journey. It makes the whole process less daunting and more rewarding.
It’s this back-and-forth, this "guess and then verify" nature, that makes finding the indefinite integral and checking the result by differentiation so engaging. It’s a problem-solving adventure with a built-in confirmation system.
You're not just memorizing formulas; you're understanding a deep relationship between two core mathematical operations. It’s like learning to ride a bike. Once you understand how pedaling (integration) makes you go and how braking (differentiation) stops you, you can navigate all sorts of terrains.
So, next time you encounter a problem that asks you to find an indefinite integral, don't just see it as a task. See it as an invitation to a mathematical investigation. Put on your thinking cap, make your best guess, and then enjoy the satisfying click when your differentiation confirms your brilliant integral. It’s a little bit of mathematical detective work that always pays off!
