Find Slope Of The Line Passing Through The Points

Hey there, awesome math adventurers! Ever looked at a graph and wondered what makes that line go up, down, or just chill out horizontally? It's all about its secret superpower, its personality, its… slope! And guess what? Finding this slope is like solving a super fun, super simple mystery, especially when you've got two points on that line to guide you. Think of it as having a treasure map, and those two points are your X marks the spot!
Imagine you're at a fantastic theme park. You've just gotten off the wildest roller coaster ever, and you're standing at the bottom of the biggest hill. Your friend, who’s a little braver (or perhaps just crazier!), is already at the very tippy-top of that same hill. You’re like, “Whoa, how steep was that climb?!” Well, that steepness, that thrilling rise, is exactly what we’re talking about with slope. It tells us how much the line goes up (or down!) for every little step it takes sideways.
Now, let's say you've got your two trusty points. Let's call them Point A and Point B. We can give them fancy names like (x₁, y₁) and (x₂, y₂). Don't let those little numbers and letters scare you! They're just like labels on a very important box. x₁ is the "sideways" number for Point A, and y₁ is the "up-and-down" number for Point A. Same deal for Point B with x₂ and y₂. Easy peasy, right?
So, how do we uncover this magical slope? It's all about finding the difference. We want to know how much we’ve gone up or down, and then how much we’ve gone sideways to get there. Think of it like this: How much did your friend climb vertically from where you are to the top of the hill? That’s the “rise.” And then, how much did the roller coaster track travel horizontally during that climb? That’s the “run.”
The super-duper, incredibly simple formula for slope is: Rise over Run!
In our fancy math talk, the "rise" is the difference in the y values (the up-and-down numbers). So, we take the y value of our second point and subtract the y value of our first point: y₂ - y₁. This tells us how much the line has changed in the vertical direction. Did it go up a lot? Did it go down a little? This little calculation will tell you!

And the "run"? That's the difference in the x values (the sideways numbers). We do the same thing: take the x value of our second point and subtract the x value of our first point: x₂ - x₁. This tells us how much the line has changed in the horizontal direction. Did it move a long way to the right? Or just a tiny bit to the left?
So, put it all together, and you’ve got our glorious slope formula: (y₂ - y₁) / (x₂ - x₁). It’s like a secret handshake for lines! You just plug in your numbers, do a little subtraction, and a little division, and BAM! You’ve got the slope.
Let’s try a super fun example. Imagine you’re at the ice cream shop (Point A!) and you decide to walk to the park (Point B!). Your ice cream shop is at coordinates (2, 3) – you know, 2 steps to the right and 3 steps up from the corner. The park is a bit further, at (6, 9) – 6 steps to the right and 9 steps up.
So, our Point A is (x₁, y₁) = (2, 3) and our Point B is (x₂, y₂) = (6, 9).
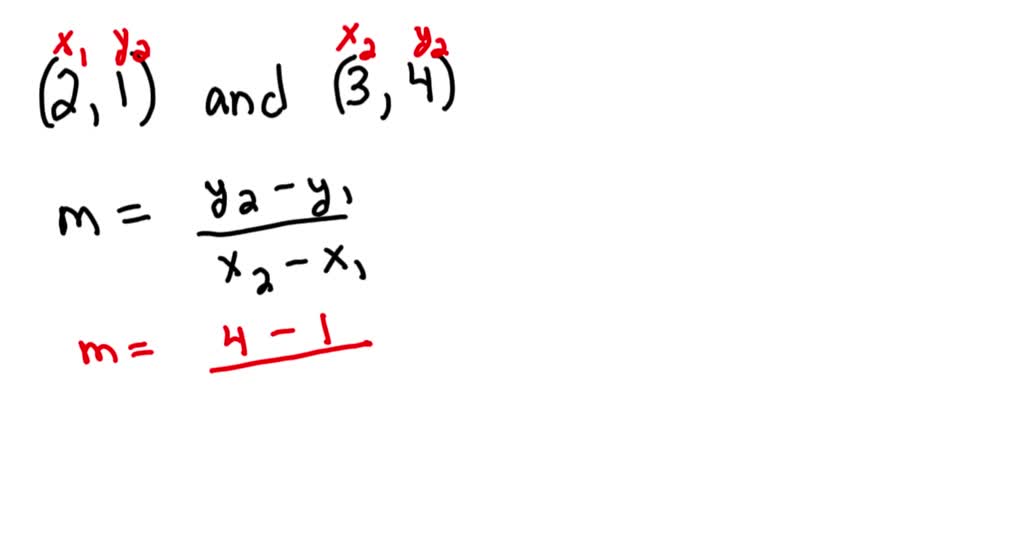
Let’s find the rise: y₂ - y₁ = 9 - 3 = 6. You walked 6 steps upwards from the ice cream shop to get to the park's elevation! Amazing!
Now, let’s find the run: x₂ - x₁ = 6 - 2 = 4. You walked 4 steps sideways to get from the ice cream shop's horizontal position to the park's horizontal position. Impressive!
Now, for the grand finale, the slope! It's rise over run, so 6 / 4. We can simplify that to 3/2, or even 1.5. This means for every 2 steps you move sideways, you go 3 steps up! Or, for every 1 step sideways, you go 1.5 steps up. This line is definitely going uphill – like a rocket to the moon!

What if the numbers are negative? No sweat! Imagine walking downhill on a ski slope. Your friend is at the top (say, 5, 5) and you’re at the bottom (say, 8, 1). That's a different kind of adventure!
Point A: (x₁, y₁) = (5, 5) Point B: (x₂, y₂) = (8, 1)
Rise: y₂ - y₁ = 1 - 5 = -4. Oh dear, you’ve gone down 4 steps! That's a negative rise, which we call a fall.
Run: x₂ - x₁ = 8 - 5 = 3. You’ve moved 3 steps to the right.
Slope: -4 / 3. So, for every 3 steps you move to the right, you're dropping 4 steps down. This line is definitely heading downhill, faster than a runaway snowball!
And what about a perfectly flat line? Like a lazy river? That means the y values are the same! If y₂ - y₁ equals 0, then the slope is 0. It’s got no steepness, it’s just cruisin’ along.
What about a perfectly vertical line, like a super-tall skyscraper? That means the x values are the same! If x₂ - x₁ equals 0, then you're trying to divide by zero. Uh oh! That's like trying to find a unicorn – it's undefined! Vertical lines have an undefined slope. They are just too steep to measure!
See? Finding the slope of a line passing through two points is like being a detective, but instead of clues, you've got numbers. And instead of a magnifying glass, you've got a simple formula. It's that easy, that fun, and that… mathematical! Go forth and conquer those lines!
