Find Polar Equation Given Eccentricity And Directrix Calculator
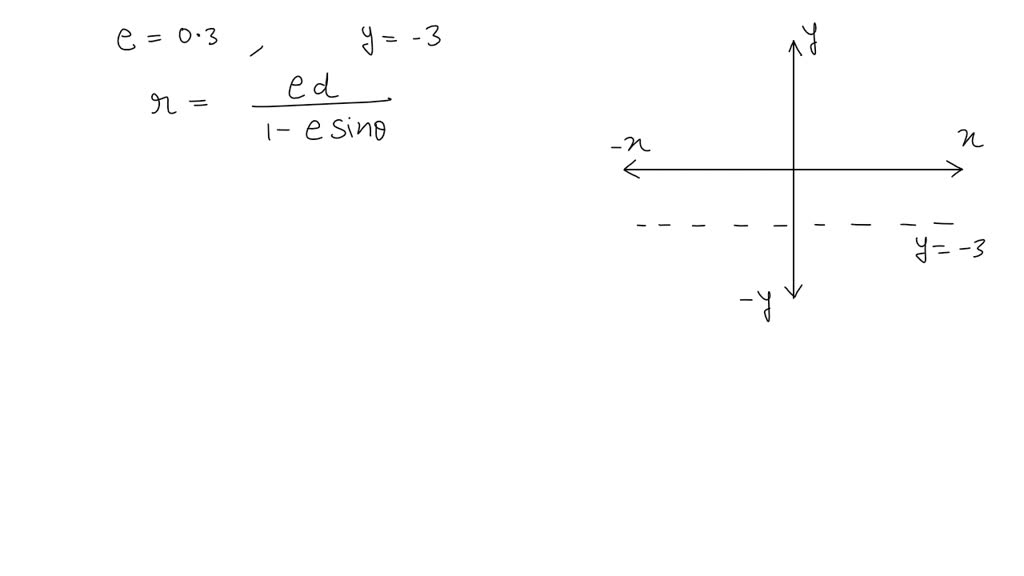
Ever looked up at the night sky and wondered about those swirling galaxies or the elliptical paths of planets? Or maybe you’ve stumbled upon some fancy-sounding math in a science documentary and thought, "What's the point of all that?" Well, buckle up, because we’re about to talk about something that connects those cosmic wonders to, believe it or not, our everyday lives – and how a handy little tool can make understanding it a breeze. We're diving into the world of polar equations, and specifically, how to find them when you’ve got a couple of key pieces of information: the eccentricity and the directrix.
Now, I know what you might be thinking. "Polar equations? Eccentricity? Directrix? Sounds like something only rocket scientists or math professors need to worry about!" And while it's true that these concepts are super important in fields like astronomy and physics, the underlying idea is actually quite… well, relatable. Think of it like this: everything in the universe has a story, and sometimes, to understand that story, we need a special kind of map. Polar equations are like a special map for curves, and the eccentricity and directrix are like the secret clues that tell us exactly what kind of curve we're dealing with and where it's going.
Let's break down these terms with a little everyday magic. Imagine you’re baking cookies. You’ve got a recipe, right? This recipe tells you the ingredients and the steps to get a delicious result. In our case, the polar equation is the final cookie – the shape itself. The eccentricity is like the texture of your cookie. Is it going to be perfectly round and smooth like a shortbread (think of a circle, where eccentricity is 0)? Or will it have a bit more of a chew, maybe slightly oval, like a classic chocolate chip cookie (eccentricity between 0 and 1, a lovely ellipse)? Or, are we talking about a super crispy, thin cookie that spreads out wide, almost like it’s trying to escape the baking sheet (eccentricity greater than 1, a hyperbola)? The eccentricity tells us how squished or stretched out our curve is going to be.
And what about the directrix? This one is a bit like the "magnetic pull" of your baking inspiration. Imagine you're a kid trying to draw a perfect circle freehand. You might imagine a tiny dot in the center (that’s your focus, which we’ll get to!) and then try to keep your pencil the same distance from that dot as you do from an imaginary line you’ve drawn off to the side (that’s your directrix). The directrix, along with the focus, helps define the shape. It’s a reference line that the curve "behaves" in relation to. For planets orbiting the sun, the sun is a focus, and the path it takes is an ellipse. For something like a comet streaking across the sky, its path might be a parabola or even a hyperbola, and these paths are also defined by a focus and a directrix.
Why Should You Care About This Mysterious Calculator?
Okay, so we’ve got the cookie analogy and the cosmic analogies. But why would an everyday person ever need to find a polar equation using eccentricity and a directrix? Here’s where the fun really starts. It’s about understanding the world around us, even the bits we don’t always consciously notice.

Think about the way water flows. A tiny ripple on a pond might look like a simple wave, but the underlying mathematical patterns are often described by these types of curves. Or consider how engineers design things. They need to understand the forces at play and how objects will move. A bridge’s arch, the path of a thrown ball, the design of a satellite dish – all these involve principles that can be described using conic sections (which are what we get when we play with eccentricity and directrix).
But let's bring it even closer to home. Imagine you’re planning a road trip. You’ve got your GPS, which is basically using complex algorithms to figure out the fastest or most efficient route. While it’s not directly calculating polar equations, the principles of describing paths and distances are fundamental. Understanding how curves are defined can make us appreciate the sophistication behind the technology we use every day.

And let’s be honest, it’s also about the joy of discovery! Learning something new, even if it seems a bit abstract at first, can be incredibly rewarding. It’s like learning a new skill, like knitting or playing an instrument. You start with the basics, and soon you’re creating something beautiful and intricate.
Enter the Calculator: Your Friendly Math Sidekick
So, how do we actually find these polar equations when we're given the eccentricity and directrix? Traditionally, this involved some careful algebraic manipulation, sketching, and a good dose of number crunching. It was the kind of thing that might make you want to hide under your duvet.

But now? We have calculators! Specifically, calculators designed to find polar equations given eccentricity and directrix. These are like having a super-smart, incredibly patient math tutor at your fingertips. You punch in the numbers – the value for eccentricity (let’s say, e) and information about the directrix (like its distance from the focus and whether it’s horizontal or vertical) – and poof! The calculator spits out the polar equation for you. It’s like having a magic wand for math!
A Little Story: The Comet's Journey
Let me tell you a little story to illustrate. Imagine a curious young astronomer, let's call her Clara. Clara spots a new comet in the night sky. She’s fascinated by its long, sweeping path. Using her telescope and some careful measurements, she figures out two crucial things about the comet's orbit: its eccentricity (how stretched out it is, let’s say it's 1.5, meaning it's not coming back) and the position of its directrix (a line far out in space that dictates how the comet moves). Clara wants to write down the exact mathematical description of this comet's path so she can predict where it will be in the future. Without a calculator, this would be a long, drawn-out process, involving geometry and algebra. But with a polar equation calculator, she can input her measurements for eccentricity and the directrix, and instantly get the equation that precisely describes the comet’s trajectory.

Suddenly, that abstract math becomes a tangible thing – the path of a celestial wanderer! And this isn't just for comets. Imagine designing a roller coaster. The thrilling loops and dips are all based on curves. Understanding how to define these curves mathematically, even if you’re not the one doing the calculation by hand, helps us appreciate the engineering marvels around us.
The beauty of these calculators is that they demystify the process. They take what can seem like intimidating mathematical jargon and turn it into a practical tool. It’s about making complex ideas accessible and allowing more people to engage with the fascinating patterns of the universe, from the grand sweep of galaxies to the intricate dance of planets, and yes, even the satisfying shape of a perfectly baked cookie.
So, the next time you hear about eccentricity or a directrix, don't shy away. Think of it as a secret code to understanding shapes. And if you're feeling adventurous, go find yourself one of these polar equation calculators. You might just discover a new way to see the world, one curve at a time!
