Find Any Numbers For Which The Rational Expression Is Undefined

Hey there, math explorers! Today, we're diving into something super cool, a little like being a detective for numbers. We're going to figure out when those tricky rational expressions decide to throw a fit and become totally undefined. Think of it as finding the Achilles' heel of an algebraic fraction.
Now, before you start picturing angry numbers or mathematical tantrums, let's calm down. It's not that dramatic! It's all about a very specific, and actually quite simple, rule that can make a fraction go "nope!" when it comes to math.
The Forbidden Zone: Division by Zero!
You know how they say "don't divide by zero"? It's like the golden rule of arithmetic. It's not just a suggestion; it's a mathematical law etched in stone (or at least in very well-respected textbooks). Why? Because it just breaks everything. Imagine trying to share 5 cookies among 0 friends. It just doesn't compute, right?
Well, the same principle applies to our fancy rational expressions. A rational expression is basically a fraction where the top and bottom are polynomials (you know, those expressions with variables and exponents, like 3x² + 2x - 1). So, when we have a rational expression like (x + 2) / (x - 3), we've got a numerator (the top part) and a denominator (the bottom part).
Our mission, should we choose to accept it (and we totally should, it's easy!), is to find the numbers that make that denominator equal to zero. Because, as we've established, dividing by zero is a big no-no in the mathematical world. It's like a red flag, a skip button, a "do not enter" sign.
Why Does This Happen? The Denominator's Dilemma
Let's think about it this way. The denominator in a fraction is the number of equal parts you're dividing the numerator into. If your denominator is 2, you're splitting something into two equal pieces. If it's 4, you're splitting it into four. But if it's 0...
...well, how do you split something into zero pieces? It's a conceptual void! It's like asking how many unicorns are in this room that are also riding bicycles backwards. It just doesn't have a sensible answer. So, our rational expression, when its denominator hits zero, just throws its digital hands up and says, "I can't even!"
Let's Get Our Detective Hats On!
So, how do we actually find these "problematic" numbers? It's easier than you think! We just focus on the denominator of the rational expression. That's our prime suspect.

Here's the game plan:
- Identify the denominator of your rational expression.
- Set that denominator equal to zero.
- Solve the resulting equation for the variable.
That's it! The numbers you find are the ones that make the original rational expression undefined. They're the rebels, the troublemakers, the ones that break the math party.
Example Time! (No, Really, It's Fun)
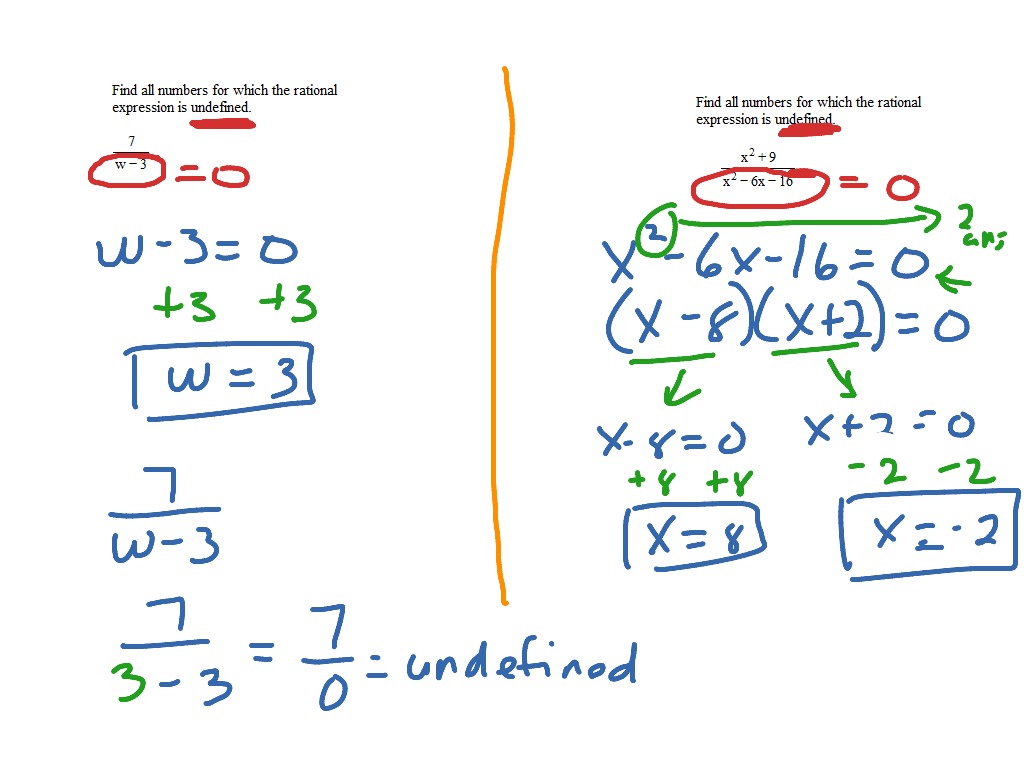
Let's take a look at our old friend, (x + 2) / (x - 3).
Step 1: Our denominator is (x - 3).
Step 2: We set it equal to zero: x - 3 = 0.
Step 3: Now, we solve for x. What do you add to -3 to get 0? That's right, +3! So, x = 3.
This means that if we plug in x = 3 into our expression, we'd get (3 + 2) / (3 - 3), which is 5 / 0. And as we know, 5 / 0 is a big fat mathematical "nope!" So, the rational expression (x + 2) / (x - 3) is undefined when x = 3.
What About More Complicated Denominators?
Okay, sometimes the denominator isn't just a simple x - a. It might be a quadratic expression, like x² - 4, or something even fancier. Does that make it harder? Nah, just a little more homework for our detective work!
If the denominator is a quadratic, we just need to solve a quadratic equation. Remember those? Factoring, using the quadratic formula – whatever works!

Example 2: The Quadratic Quandary
Let's tackle this beast: (2x + 1) / (x² - 4).
Step 1: Denominator is x² - 4.
Step 2: Set it to zero: x² - 4 = 0.
Step 3: Solve for x. This is a difference of squares, a classic! We can factor it as (x - 2)(x + 2) = 0.
Now, for this product to be zero, at least one of the factors has to be zero. So, we have two possibilities:
- x - 2 = 0 => x = 2
- x + 2 = 0 => x = -2
So, for the rational expression (2x + 1) / (x² - 4), it's undefined when x = 2 and also when x = -2. See? We've got two troublemakers this time!
Example 3: The Factoring Fun
What if we have something like (x) / (x² + 5x + 6)?
Step 1: Denominator is x² + 5x + 6.
Step 2: Set it to zero: x² + 5x + 6 = 0.
Step 3: Let's factor this quadratic. We need two numbers that multiply to 6 and add to 5. Those are 2 and 3! So, we get (x + 2)(x + 3) = 0.
Again, we set each factor to zero:
- x + 2 = 0 => x = -2
- x + 3 = 0 => x = -3
Our undefined numbers for this expression are x = -2 and x = -3. High fives all around!
What If the Denominator Never Equals Zero?
This is a great question! Sometimes, you'll get a denominator that, no matter what real number you plug in for x, will never be zero. For instance, consider (x + 1) / (x² + 1).
If we set the denominator to zero: x² + 1 = 0.
Subtracting 1 from both sides gives us x² = -1.
Now, can you think of a real number that, when squared, gives you a negative number? Nope! The square of any real number is always zero or positive. So, there are no real solutions for x² = -1.
In this case, the rational expression (x + 1) / (x² + 1) is defined for all real numbers. It's like a well-behaved citizen of the math world, never causing any trouble.
Polynomials That Are Always Positive (or Always Negative)
Sometimes, especially with quadratics, the entire polynomial might always be positive or always be negative. Think of y = x² + 3. The smallest x² can be is 0, so the smallest x² + 3 can be is 3. It never hits zero!
This is handy because if you can determine that your denominator is always going to be some non-zero value, you don't have to worry about it making your expression undefined. You can just relax and enjoy the math!
Putting It All Together: Your Undefined Number Toolkit
So, to recap our detective mission:
- The Goal: Find numbers that make a rational expression undefined.
- The Key: Division by zero is the enemy!
- The Target: Always focus on the denominator.
- The Method: Set the denominator equal to zero and solve for the variable.
- The Potential Issues: If the denominator is a simple linear expression, you'll likely get one undefined number. If it's quadratic, you could have up to two!
- The "Always Defined" Cases: Sometimes, the denominator will never equal zero for any real number.
It's all about spotting that denominator and giving it a good stare-down to see if it can be zero. If it can, those are your forbidden numbers!
A Little Reminder About Context
It's worth noting that sometimes, in more advanced math, we might talk about complex numbers. But for this level, when we're finding numbers for which a rational expression is undefined, we're typically talking about real numbers.
So, when we say x² = -1 has no real solutions, that's our cue that the expression is defined for all the numbers we usually care about (the real ones).
The Joy of Understanding!
See? It's not scary at all! It's just a simple rule about avoiding that pesky division by zero. Every time you find these "undefined" numbers, you're not finding a problem, you're actually gaining understanding. You're learning the boundaries, the limits of where your mathematical tool can be used.
Think of it like learning to ride a bike. At first, you might wobble and even fall a bit. Those falls are like the undefined numbers – they show you the edge, the point where you need to be careful. But with each wobble and each brush-off, you learn to balance better and ride further.
So, the next time you see a rational expression, don't shy away from it. Embrace the challenge! Grab your detective hat, sharpen your pencil, and go find those numbers. You’ve got this! You're not just solving problems; you're unlocking the secrets of mathematics, one denominator at a time. And that, my friends, is pretty darn awesome. Keep exploring, keep learning, and keep smiling as you conquer these mathematical puzzles!
