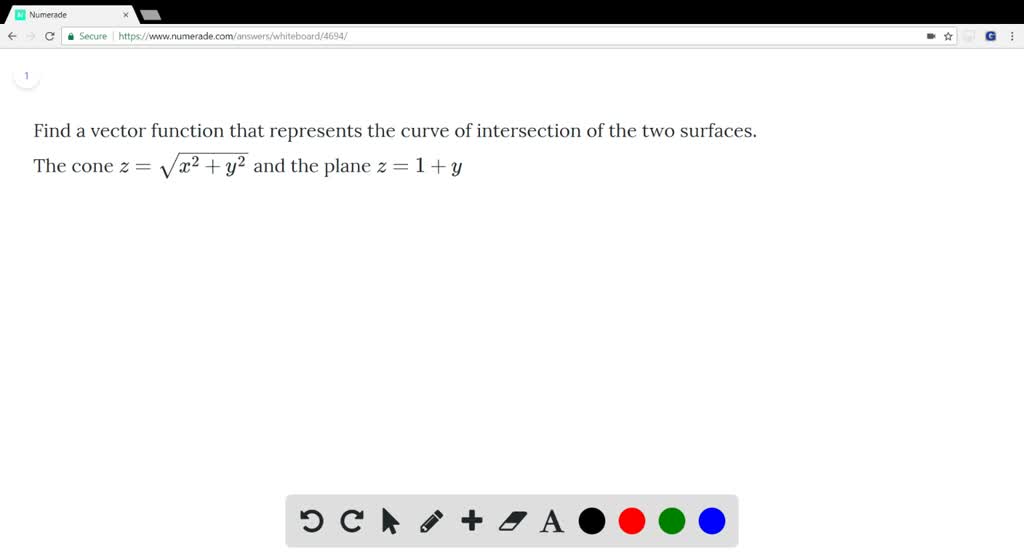
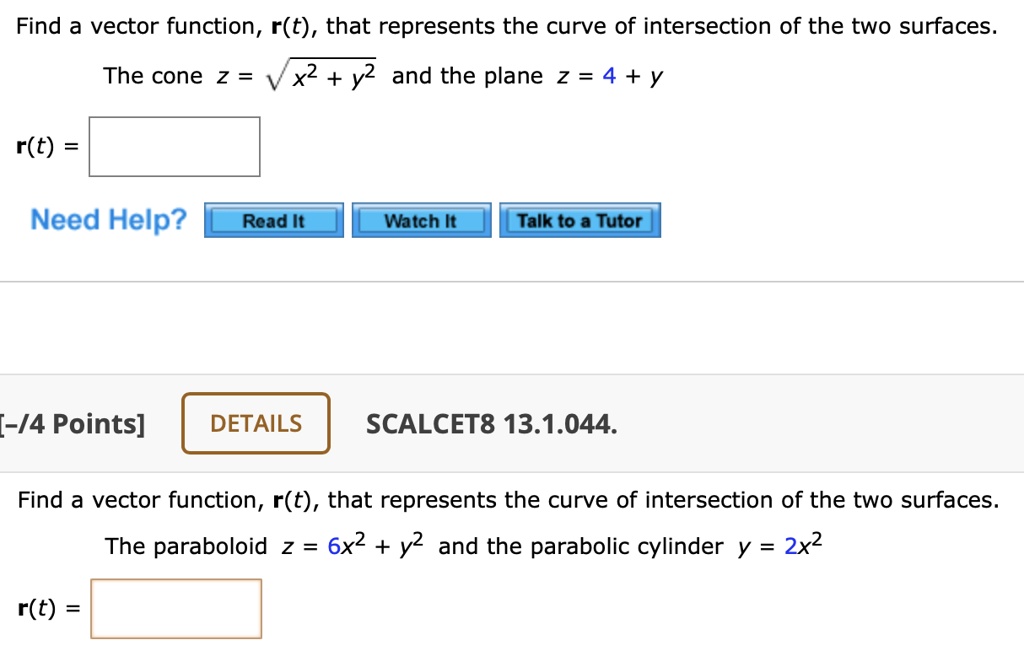
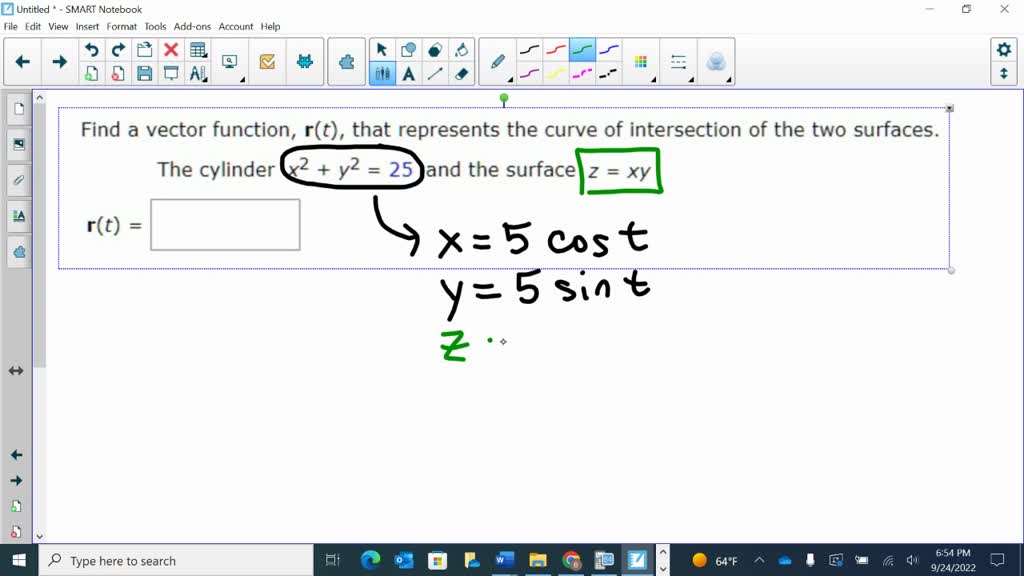
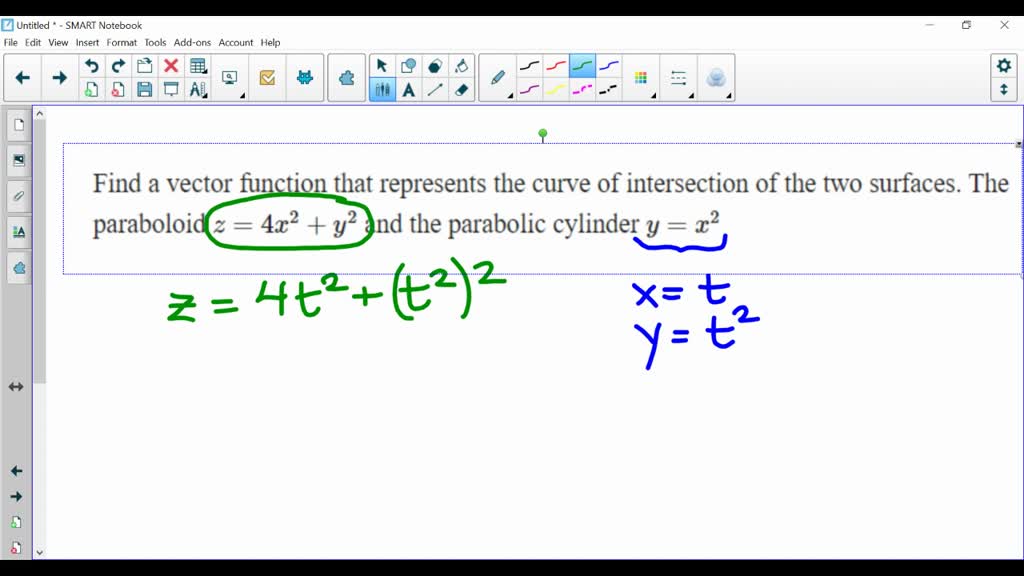
Find A Vector Function That Represents The Curve Of Intersection

Imagine you have two cool shapes, like a shiny sphere and a swirly tube. Now, what happens when they bump into each other? Where they cross paths creates a brand new shape!
Finding a vector function that describes this crossing shape is like giving that new shape its own secret code. It’s a way to trace its every twist and turn perfectly.
Think of it like drawing a treasure map. This vector function is the map that shows you exactly where the intersection curve is, step by step.
It’s not just about finding the shape; it's about understanding its journey. A vector function tells us how to travel along that curve, one point at a time.
This whole idea is super neat because it blends geometry and algebra. It’s like having a secret handshake between two different branches of math!
You’re taking the real-world shapes we can see and touch, and describing them with abstract math.
And the "curve of intersection" itself? It's often something quite beautiful. It’s not just a simple line; it can be an elegant loop or a complex spiral.
It’s like nature showing off its artistic side! These intersection curves are the hidden masterpieces of geometry.
So, how do we actually find this magical vector function? Well, it involves a bit of clever thinking and some math magic.
We start with the equations that define our original shapes. Let’s say we have a sphere defined by one equation and a plane by another.
The points that lie on both the sphere and the plane are the points of intersection. This is the key!
We want to find a way to list all those shared points using a single parameter, usually a variable like 't'.
This parameter 't' acts like a timer. As 't' changes, our vector function gives us a new point on the intersection curve.
It's like pressing "play" on a movie. The parameter 't' is the movie's timeline, and the vector function is the director telling the camera where to move.
If our sphere is x² + y² + z² = 25 and our plane is, say, z = 3, the intersection points must satisfy both.
Substituting z = 3 into the sphere equation gives us x² + y² + 9 = 25. This simplifies to x² + y² = 16.
This new equation, x² + y² = 16, describes a circle of radius 4 in the plane where z = 3.
Now, how do we represent this circle as a vector function? We can think of its x and y coordinates.
We know that a circle of radius r in the xy-plane can be written as x = r cos(t) and y = r sin(t).
In our case, the radius is 4. So, we can set x = 4 cos(t) and y = 4 sin(t).
And what about z? We already know that for all points on our intersection, z = 3.
So, our vector function, let's call it r(t), can be written as: r(t) = <4 cos(t), 4 sin(t), 3>.
This is it! This simple-looking formula describes a perfect circle in 3D space.
As 't' goes from 0 to 2π, cos(t) and sin(t) trace out a full circle. And the 3 at the end keeps us firmly on that specific plane.
What makes this so entertaining? It's the satisfaction of cracking a puzzle. You take two complex surfaces and boil down their meeting point to a elegant, manageable curve.
It’s like finding a hidden gem. You’re not just seeing the intersection; you're defining it with mathematical precision.
And the "special" part? It’s the realization that these abstract equations can perfectly mimic real-world or imagined shapes.
It bridges the gap between our imagination and the language of mathematics.
Consider other, more complex intersections. What if we intersect a cylinder with a parabolic surface? The resulting curve can be far more intricate.
Finding the vector function for those is a more involved process, but the thrill of discovery is even greater.
It often involves clever substitutions and a good understanding of parametric equations.
Sometimes, the parameter 't' isn't as obvious as an angle. It might be a variable directly related to one of the coordinates, or something else entirely.
The goal is always the same: to express the x, y, and z coordinates of every point on the intersection curve as functions of a single parameter.
This process is incredibly useful in fields like computer graphics, physics, and engineering.
Imagine designing a car. The smooth curves of the body panels are often defined by such intersection curves.
Or in video games, the complex shapes of characters and environments are built using these mathematical principles.
It's the secret sauce that makes digital worlds look so realistic and engaging.
So, next time you see a sleek design or a beautifully rendered curve, remember the math behind it.
Remember the journey of finding that vector function, the secret code that brings a curve of intersection to life.
It’s a testament to the power of mathematics to describe and create beauty.
It’s a wonderful example of how abstract concepts can have tangible, even artistic, applications.
The process itself is a form of problem-solving that can be incredibly rewarding.
You start with a question: "Where do these two shapes meet?" And you end with a precise answer: a beautiful, mathematically defined curve.
The elegance of the solution is often as impressive as the curve itself.
It's a little bit like detective work, but instead of clues, you're using equations.
And the treasure you find? It's the perfect description of a fascinating shape.
The beauty of a vector function is its ability to describe motion or a path. It’s not just a static shape; it’s a recipe for drawing that shape.
This makes it incredibly powerful for understanding how things move or how paths are formed.
Think about designing a roller coaster. The track is a complex curve, and understanding its shape with vector functions is crucial for safety and thrill.
It’s this blend of static description and dynamic potential that makes finding these functions so captivating.
So, if you ever feel a pull towards understanding how shapes interact or how beautiful curves are made, dive into the world of vector functions.
It’s a realm where imagination meets the precision of mathematics, and the results are always something special.
You'll discover a new way to see the world, a world defined by the elegant dance of intersecting surfaces.
It’s a fascinating pursuit that can unlock a deeper appreciation for the geometry all around us.
And who knows, you might just find yourself creating some mathematical art of your own!
The exploration of these curves is a never-ending adventure in mathematical discovery.
It’s a delightful challenge that offers a unique perspective on spatial relationships.
So, embrace the fun of solving these mathematical puzzles!
It’s a journey that’s both intellectually stimulating and visually rewarding.
You are essentially creating the DNA for a beautiful mathematical object.
And that, in itself, is pretty awesome.
It’s about understanding the essence of where things meet.
And that essence can be expressed in a surprisingly simple and elegant way.
The ability to translate visual intersections into algebraic expressions is a fundamental magic.
It’s like having a superpower for geometry.
It allows us to model and understand complex relationships in space.
The process is an exercise in logical deduction and creative problem-solving.
It’s a way of giving form and structure to abstract ideas.
And the outcome is a precise description of a shape’s meeting point.
It’s a beautiful fusion of analytical and synthetic thinking.
This is why finding a vector function for the curve of intersection is so engaging and special.
