Expand And Simplify X 6 X 2: Complete Guide & Key Details
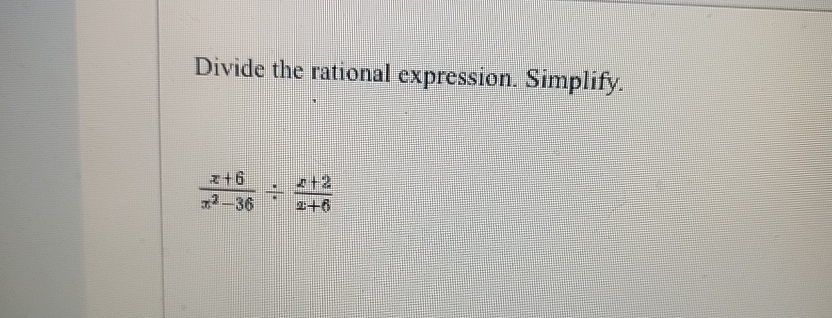
Hey there, fellow curious minds! Ever find yourself staring at a math problem that looks like a tangled ball of yarn and thinking, "Is there a simpler way to unravel this?" Well, today, we're going to tackle exactly that. We're going to dive into the seemingly simple yet surprisingly powerful world of expanding and simplifying expressions, specifically one that might pop up in your math adventures: X 6 X 2. Sounds a bit like a secret code, right? Let's decode it together!
So, what exactly are we talking about when we say "expand and simplify"? Think of it like this: have you ever gotten a gift wrapped in tons of fancy paper and ribbons? Expanding is kind of like carefully unwrapping all those layers to see what's inside. Simplifying, on the other hand, is like taking all those loose bits and pieces and putting them neatly back into a single, easy-to-understand package. In math, expanding means getting rid of parentheses by multiplying, and simplifying means combining similar terms to make the whole thing shorter and sweeter.
Unpacking the Mystery of X 6 X 2
Now, let's zoom in on our specific expression: X 6 X 2. At first glance, it might seem a little ambiguous. Is it X multiplied by 6, then multiplied by 2? Or is it X multiplied by the sum of 6 and 2? Or maybe something else entirely? In the wild world of algebra, when you see numbers and variables right next to each other like this, it almost always means multiplication. So, X 6 X 2 is actually a shorthand for X * 6 * 2.
It’s a bit like seeing "NYC" instead of "New York City." We just understand what it means. In this case, X 6 X 2 is the same as X times 6 times 2.
The "Expand" Part: Making it Bigger (Temporarily!)
So, how do we "expand" this? Well, in this particular case, there aren't any parentheses to deal with, which is a bit of a head-start! Expanding here is more about performing the multiplications that are already implied.
We have X, then we have the number 6, and then we have the number 2. Multiplication is friendly because it doesn't matter which order you do it in – you'll always get the same answer. This is thanks to something super neat called the commutative property of multiplication. It's like saying you can put your socks on before your shoes, or your shoes before your socks, and you still end up with feet that are ready to go!
So, we can multiply the numbers first: 6 * 2. What does that give us? Yep, you guessed it: 12.
Now, we just have X left to deal with, and our 12. So, the expanded form, with the numbers multiplied together, is X * 12.
Easy peasy, right? We've basically just tidied up the numbers.
The "Simplify" Part: Making it Smaller and Neater
This is where the real magic happens! Simplifying is all about making expressions as concise as possible. In our case, we've already done a lot of the simplifying by performing the multiplication of 6 and 2.
We had X * 6 * 2. We performed the multiplication of the constants (the numbers) and got 12. So, we ended up with X * 12.

Now, in algebra, we have a convention. When we have a variable multiplied by a number, we usually write the number first, followed by the variable. So, X * 12 is more commonly written as 12X. It's just the standard way of writing things down, like how we read from left to right.
So, the simplified form of X 6 X 2 is simply 12X.
Isn't that cool? We took something that looked like it had a few steps to it, and with a little bit of understanding about multiplication and how we write things in algebra, we turned it into something much more streamlined.
Why Does This Even Matter?
You might be thinking, "Okay, that's neat, but why should I care about expanding and simplifying things like X 6 X 2?" Great question! Think of it as building a strong foundation for more complex math. If you can confidently handle these simple steps, you'll be way ahead when you start tackling more intricate equations and problems.
Imagine you're building with LEGOs. If you can easily connect a few basic bricks, you're ready to build anything from a small car to a giant castle. Expanding and simplifying are those basic LEGO bricks of algebra. They help us break down complex problems into manageable parts.

Furthermore, in real-world applications, you'll often encounter equations that need to be simplified to make sense of data or to find solutions. Whether it's calculating the cost of multiple items, figuring out distances, or even in coding, being able to simplify expressions is a fundamental skill.
A Little More on Simplifying: Combining Like Terms
While our example X 6 X 2 was pretty straightforward, let's briefly touch on a slightly more complex scenario to really drive home the "simplifying" idea. What if you had an expression like 3X + 5X + 7?
Here, the "like terms" are the ones that have the same variable part. In this case, 3X and 5X are like terms because they both have an X. The number 7 is by itself, so it's a "constant" term.
To simplify, we combine the like terms. We can add the coefficients (the numbers in front of the variables): 3 + 5, which equals 8. So, 3X + 5X becomes 8X.

Then, we bring in our constant term: 8X + 7. Since 8X and 7 are not like terms (one has an X, the other doesn't), we can't combine them any further. So, the simplified form is 8X + 7.
See? We took a slightly longer expression and made it shorter and easier to read. It’s like decluttering your desk – everything is in its place and you can find what you need in a flash!
Key Takeaways: Your Cheat Sheet
Let's wrap this up with the most important bits. When you see something like X 6 X 2, remember:
- It means
X * 6 * 2. - The numbers can be multiplied together first because of the commutative property.
6 * 2 = 12.- The expression becomes
X * 12. - We write this in the simplified form as
12X.
Expanding and simplifying are not just about solving math problems; they're about developing a clearer, more efficient way of thinking. They teach us to break things down, to find patterns, and to express ideas in the most direct way possible.
So, the next time you encounter an expression that looks a little daunting, take a deep breath, remember these simple steps, and go forth and conquer! You've got this!
