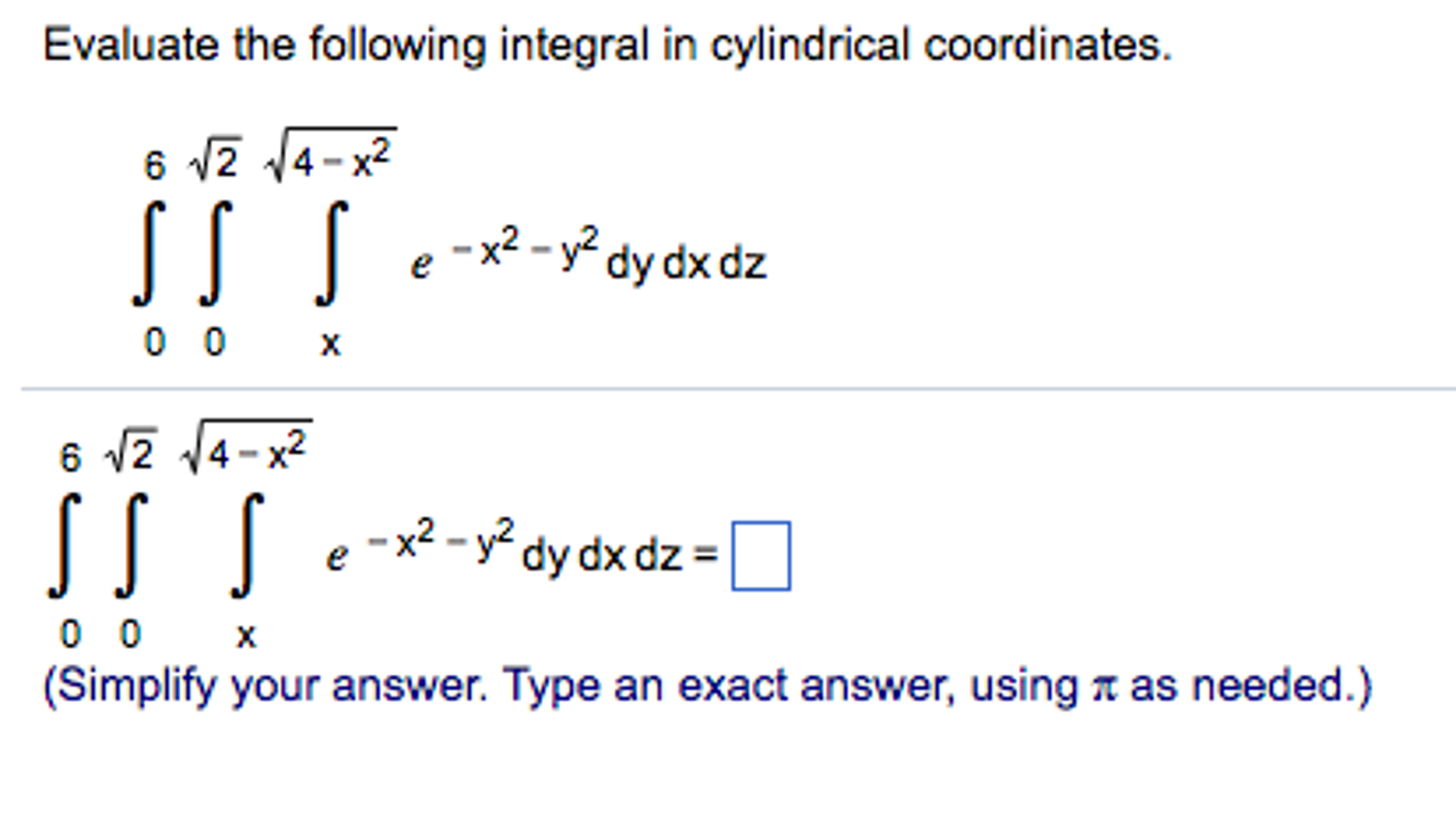
Evaluate The Following Integral In Cylindrical Coordinates.
Oh, you know, calculus. It’s that thing we all vaguely remember from school, right? The one with all the squiggly lines and funny symbols. And sometimes, they throw in these things called "integrals." They're like really, really complicated sums.
And then, just when you think you've got a handle on it, they introduce a new way to look at things. We’re talking about cylindrical coordinates today. It’s like deciding to measure your house by how many pizzas fit in it instead of by feet. Utterly delightful, isn't it?
So, we have this integral. It’s a bit of a beast, to be honest. And we’re supposed to evaluate it. In cylindrical coordinates, no less! It’s like being asked to bake a cake using only a shoe and a spoon.
Let's call our trusty integral “Big Bertha.” She's not the prettiest function, but she's got depth. And we need to figure out her total volume, or area, or whatever it is we're measuring here. It’s all very… mathematical.
Now, cylindrical coordinates. Imagine a can of soup. That’s basically it. You’ve got your radius, the distance from the center. Then you’ve got your angle, like how you’d twist the can. And of course, there’s the height, simple enough.
So, our problem says: "Evaluate The Following Integral In Cylindrical Coordinates." It’s a command, you see. A challenge! A dare, almost. And I, for one, accept! Mostly because I have to.
The integral itself looks like a secret code. ∫∫∫. Three of them! That means we’re going deep. We’re not just dipping our toes; we’re going for a full-on swim in the mathematical ocean. And this ocean is shaped suspiciously like a stack of pancakes.
The function we're integrating is something like f(x, y, z) = x² + y². See that x² + y²? In the world of geometry, that's like a secret handshake for circles. It screams "radius squared" from the rooftops.
And what do you know, cylindrical coordinates have a little thing called ‘r’. And our integral is all about r². It's like they were made for each other, destined to be together in this mathematical dance. It's almost poetic, if you squint hard enough.

So, the x and y from the original integral? They’re going to transform. They’re going to become their cylindrical selves. It's like a superhero origin story, but with math. They shed their old identities and embrace their new powers.
The transformation rule is pretty simple, really. x = r cos(θ) and y = r sin(θ). Remember those from trigonometry? They’re back to haunt us! But this time, they're our friends, our guides. Our mathematical sidekicks.
And that x² + y²? Boom! It becomes r². Just like that. Poof! Magic! It’s so clean, so elegant. It makes you wonder why we bother with x and y in the first place.
But wait, there's more! When you switch to cylindrical coordinates, you don't just swap variables. You have to account for the "volume element." It's like when you change currency; you need an exchange rate. Here, it’s dV = r dz dr dθ.
See that extra ‘r’? It’s the unsung hero. It’s the tip for the waiter, the tax on the purchase. It’s crucial. Without it, our entire calculation would be off. A mathematical faux pas of epic proportions.
So, our integral, which looked scary before, now starts to look… manageable. Even a little bit… fun? (Don't tell anyone I said that). It’s like seeing a tangled ball of yarn and then finding the end to start unraveling it.
The limits of integration are also super important. These tell us where our can of soup starts and ends. What's the radius? What's the angle range? What's the height? We need all these details.

Let's say the region is a nice, clean cylinder. From z=0 to z=10. Radius from 0 to 5. And the angle goes all the way around, from θ=0 to θ=2π. A full circle, a complete revolution.
So, the integral transforms into something like: ∫(from 0 to 2π) ∫(from 0 to 5) ∫(from 0 to 10) r² * r dz dr dθ.
This simplifies to: ∫(from 0 to 2π) ∫(from 0 to 5) ∫(from 0 to 10) r³ dz dr dθ.
Now, we integrate with respect to z first. Since r³ is just a constant with respect to z, the integral of r³ from 0 to 10 is just 10r³. Easy peasy.
Next, we integrate with respect to r. We have the integral of 10r³ from 0 to 5. This is like finding the area under a curve that’s getting steeper and steeper. It's 10 times (r⁴/4) evaluated from 0 to 5.
Plugging in 5, we get 10 * (5⁴/4) = 10 * (625/4) = 6250/4 = 3125/2. Not bad. This is the result of our middle integral.
Finally, we integrate with respect to θ. We have the integral of 3125/2 from 0 to 2π. Since 3125/2 is a constant, it's just (3125/2) * θ evaluated from 0 to 2π.

Plugging in 2π, we get (3125/2) * 2π = 3125π.
And there you have it! 3125π. The answer to our intimidating integral, all thanks to the magic of cylindrical coordinates. It’s like solving a Rubik’s Cube, but with numbers.
It’s funny, isn't it? How changing your perspective can make something so complex seem so… neat. It’s like putting on glasses and suddenly realizing all those blurry shapes were actually interesting things.
So, the next time you see an integral that looks like a tangled mess, remember the cylindrical coordinate option. It’s the superhero cape that swoops in and saves the day. Or at least makes the calculations a little less painful.
And hey, if you can explain it using pizza slices and soup cans, even better. That’s the kind of math I can get behind. The kind that doesn't make your brain feel like it's trying to divide by zero.
So, let’s raise a metaphorical glass to cylindrical coordinates! They might be tricky to get used to, but they’re the unsung heroes of many a calculus problem. They make the impossible, well, calculable.
And that’s all there is to it. A little bit of transformation, a little bit of integration, and a whole lot of… math. But this time, it wasn’t so bad, was it? Dare I say, it was almost… enjoyable?

Perhaps my unpopular opinion is that sometimes, these mathematical transformations are actually kind of cool. They’re like a puzzle where all the pieces suddenly click into place. And the final picture is… well, a number.
This entire process feels a bit like trying to find your car keys in a very dark room. You know they're there, but you need the right flashlight. Cylindrical coordinates are that flashlight for certain integrals.
So, when faced with a daunting integral, take a deep breath. Think about the shape. Does it look like a stack of coins? A slice of cake? If so, cylindrical coordinates might just be your new best friend.
And if you’re still confused, just picture that can of soup. Radius, angle, height. It’s not so scary when you relate it to something you can hold. Or eat.
Ultimately, evaluating integrals in cylindrical coordinates is about embracing a new way of seeing. It’s about letting go of the familiar and stepping into a more descriptive space. A space where x² + y² becomes a simpler r².
It's a mathematical upgrade. Like going from dial-up internet to broadband. Suddenly, everything is faster and more efficient. Your brain will thank you. Probably.
And the final answer, 3125π, it’s just a number. But it represents something real. The volume, or whatever it is, of that specific mathematical space. It's the culmination of our little adventure.
So, next time you encounter an integral that makes you want to run for the hills, remember the power of perspective. Remember the elegance of cylindrical coordinates. And remember that even the most complex math can be broken down, simplified, and perhaps, just perhaps, made a little bit fun. Especially if you think about soup.
