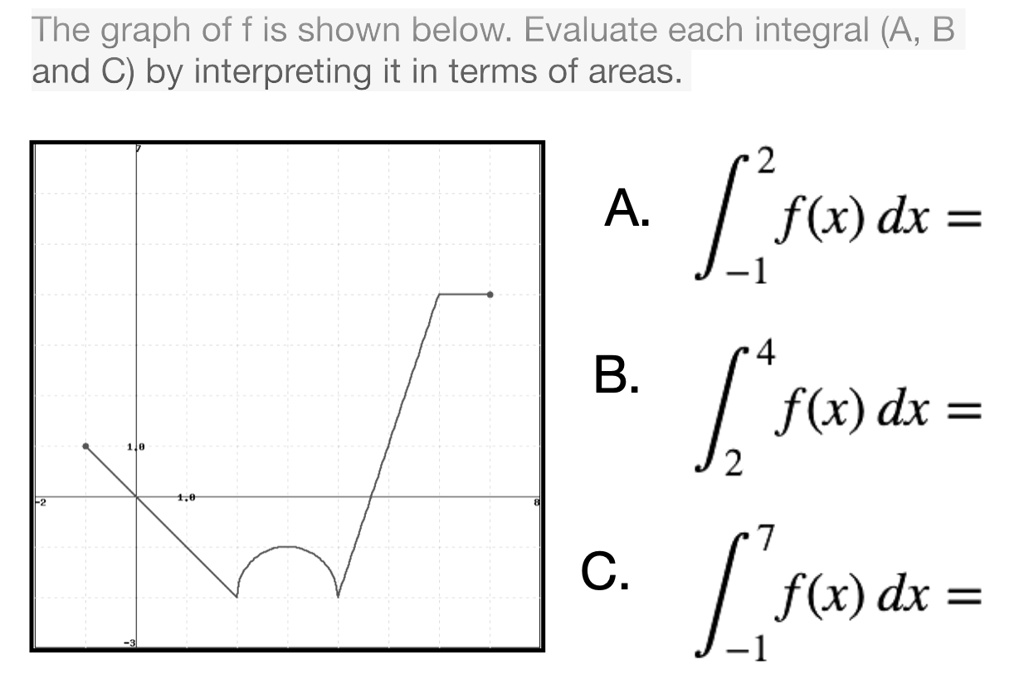
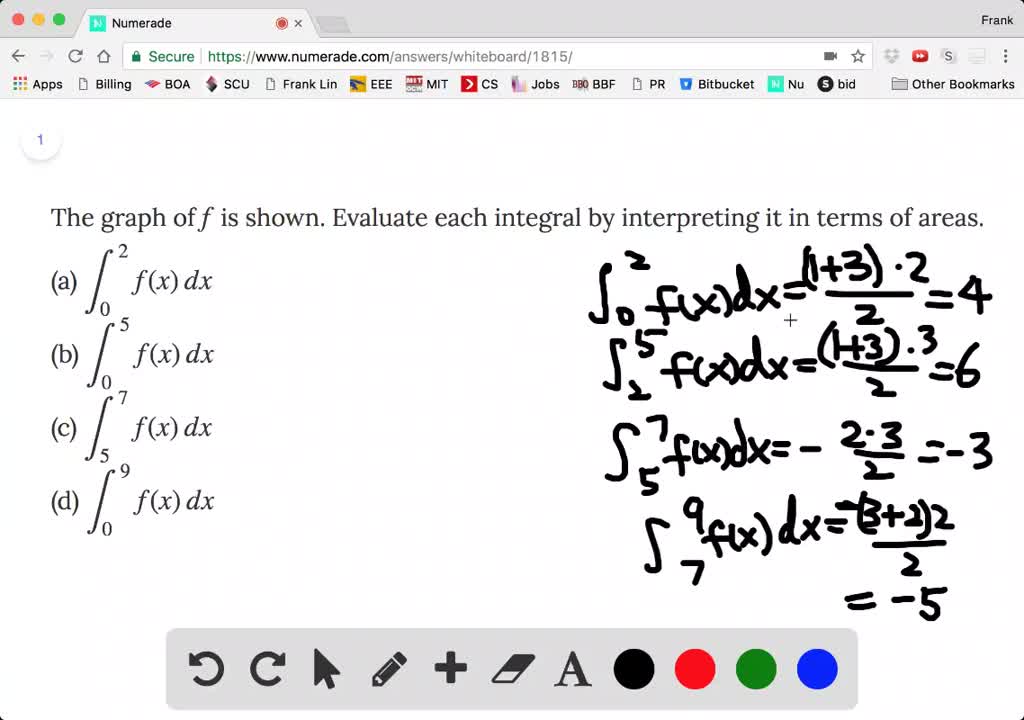
Evaluate Each Integral By Interpreting It In Terms Of Areas
Alright, settle in, grab your metaphorical latte, and let's dive into the wonderfully weird world of integrals. Now, I know what you're thinking: "Integrals? Is this some kind of secret handshake for rocket scientists?" Nope! Today, we're ditching the calculus textbooks and treating these bad boys like… well, like delicious pastries that represent areas. Seriously. We're not going to be doing any namby-pamby algebraic wizardry. We're going to picture them. Think of it as a mental art class for your brain, with bonus points for giggles.
So, what's the big deal with integrals? At its core, an integral is just a fancy way of asking, "What's the total amount of something under a curve?" Imagine you're trying to figure out how much cake you actually ate from a giant, wobbly cake. That's kind of what an integral does, but for functions. And the coolest part? We can often figure this out by looking at the area. It's like a secret superpower that mathematicians have.
The Undercover Agent: Definite Integrals and Their Area Missions
Our main characters today are called definite integrals. They have these neat little boundaries, like a fence around a garden. You'll see them written something like this: ∫ab f(x) dx. That little 'a' and 'b' are your fence posts, telling you where to start and stop measuring the area. And f(x) is your curve – the wiggly line that defines the shape of your "cake."
The 'dx' at the end? Don't sweat it. It's just the mathematician's way of saying, "Hey, we're dealing with tiny, infinitesimally small slices along the x-axis." Think of it as the breadcrumbs leading you to the delicious area. For our purposes, we can mostly ignore it and focus on the shape!
Mission 1: The Straight and Narrow – Area Under a Flat Line
Let's start with the easiest one. Imagine you have a function that's just a straight, flat line. Like, f(x) = 3. And your integral is ∫14 3 dx. This means we want the area under the line y=3, between x=1 and x=4.
Now, picture this. You've got a perfectly rectangular slice of cake. The height is 3 (that's our f(x)), and the width is from 1 to 4. How wide is that? 4 minus 1, which is 3. So, you have a rectangle that's 3 units high and 3 units wide. What's the area of a rectangle? Drumroll please… base times height! So, 3 * 3 = 9. Ta-da! The integral ∫14 3 dx equals 9. Easy peasy, lemon squeezy. This is so simple, even a toddler could grasp it, if they were motivated by more than just throwing blocks.

Mission 2: The Gentle Slope – Area Under a Diagonal Line
Okay, things are getting a little more interesting. What if your function is a line with a bit of a slope? Let's say f(x) = x. And we want to find ∫02 x dx. This means we're looking at the area under the line y=x, from x=0 to x=2.
What shape do you get here? When you draw a line from (0,0) to (2,2) and then go down to the x-axis, you get… a triangle! Specifically, a right-angled triangle. The base of our triangle is from x=0 to x=2, so it's 2 units long. The height of the triangle, at x=2, is f(2) = 2. So, the height is 2 units.
What's the area of a triangle? It's half times base times height. So, (1/2) * 2 * 2 = 2. Boom! The integral ∫02 x dx is 2. See? We're just identifying shapes and using their area formulas. It's like a geometric scavenger hunt. And who doesn't love a good scavenger hunt? Especially one that doesn't involve actual digging or the possibility of poison ivy.
Mission 3: The Curveball – Area Under a Parabola
Now, this is where it gets fun. What if your function is a curve? Think of a parabola, like f(x) = x2. Let's say we want to calculate ∫01 x2 dx. This is the area under the curve y=x2, from x=0 to x=1.

This isn't a simple rectangle or triangle. It's a smooth, swooping shape. Now, here's the tricky part. If we were to try and calculate this exactly without calculus, we'd be here all day, probably developing carpal tunnel from drawing countless tiny rectangles. But, since we're interpreting it as an area, we can think about it conceptually.
Imagine you're filling this shape with water. The integral is telling you the total volume of water that fits in there. The curve y=x2 starts at (0,0) and goes up to (1,1). The area under this curve is going to be less than the area of the square that encloses it (which would be 1x1=1). It's also going to be more than the area of the triangle we saw earlier (which was 2, but that was a different line).
The actual answer for ∫01 x2 dx is 1/3. So, this curved little sliver holds a volume of 1/3. It's like a perfectly shaped little divot. This is where the magic of calculus truly shines, but for our "interpreting as area" game, we're appreciating the visual representation. Think of it as a beautiful, slightly elusive shape on a graph.
The Tricky Bits: When Things Go Negative and Why We Should Care
What happens if our curve dips below the x-axis? Let's say we're looking at ∫-11 x dx. Here, the function is f(x) = x. Between x=-1 and x=0, the line y=x is below the x-axis. Between x=0 and x=1, it's above.
When we're interpreting as area, we have to be careful. The area above the x-axis counts as positive. The area below the x-axis counts as negative. This is a crucial detail! It's like a cosmic balance sheet for areas.
So, for ∫-11 x dx, we have a triangle below the axis from x=-1 to x=0. It has a base of 1 and a height of -1 (since it's below). Its "area" is (1/2) * 1 * (-1) = -1/2.
Then, we have a triangle above the axis from x=0 to x=1. It has a base of 1 and a height of 1. Its area is (1/2) * 1 * 1 = 1/2.
When we add these together (because the integral is asking for the total signed area), we get -1/2 + 1/2 = 0. So, ∫-11 x dx = 0. It's like the universe cancelled out the positive and negative bits. A perfectly balanced act, like a yoga instructor on a tightrope.

The Superpower Explained: Riemann Sums in Disguise
You might be wondering, "How did mathematicians even come up with this area thing?" Well, they started by approximating. Imagine chopping the area under the curve into a bunch of skinny rectangles. The more rectangles you use, the closer you get to the true area. This is the idea behind something called Riemann sums. It’s like painstakingly building a mosaic, one tiny tile at a time.
The integral is essentially the limit of these Riemann sums as the rectangles become infinitely thin. It’s a way of getting an exact answer from an infinite number of infinitesimally small approximations. Pretty mind-blowing, right? It's like using a microscopic brush to paint the universe.
So, What's the Takeaway?
When you see an integral with limits, don't panic and reach for the antacids. Visualize it. Ask yourself: What shape am I looking at? Is it a rectangle? A triangle? A curved region? And most importantly, is it above or below the x-axis?
By interpreting integrals as areas, you're not just solving math problems; you're developing a powerful geometric intuition. You're seeing the abstract beauty of calculus laid out visually. So, next time you encounter an integral, think of it as a delicious slice of mathematical pie, and enjoy the process of finding its area!
