Dilations Translations Rotations And Reflections Worksheet Answers
Hey there, curious minds! Ever looked at a cool geometric pattern or a funky design and wondered how it all came together? You know, those shapes that seem to have been stretched, slid, spun, or flipped? Well, today we're diving into the awesome world of transformations in geometry, and how a little thing called a "worksheet" can actually be your ticket to understanding this stuff. No need to break out in a sweat – we're talking about a super chill exploration of dilations, translations, rotations, and reflections.
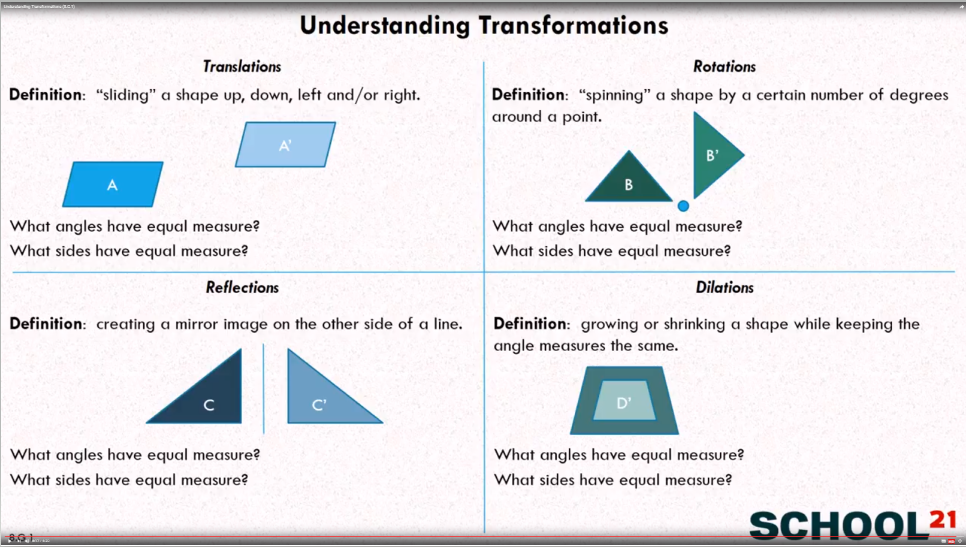
Think of these transformations like different ways to play with shapes. Imagine you have a plain old square. What can you do with it? You could make it bigger or smaller, right? That's kind of like a dilation. Or, you could slide it across the table without changing its size or direction. That’s a translation. You could also spin it around its center, like a dancer twirling. Hello, rotation! And then, you could hold a mirror up to it and see its exact opposite. That’s a reflection.
Now, why would you even care about this? Well, beyond just looking pretty in math books, these transformations are everywhere. Think about video games. How do characters move? How do objects appear or disappear? It's all about translations and rotations! Or consider animation. Flipping and resizing images is a core part of making things move on screen. Even in architecture and design, understanding how shapes can be manipulated is super important.
So, where does the "worksheet" part come in? Imagine a worksheet as your playground for these transformations. It's a space where you get to try out these moves on paper (or a screen!). And the "answers" part? That's just the magic ingredient that helps you check your work and really get a feel for what you've done. It’s like having a friendly guide showing you the ropes.
Let's Break Down the Moves!
Ready to get a little more specific? Let's chat about each of these transformations in a way that makes sense.
Dilations: The Shrink Ray and the Magnifying Glass
Okay, so dilations are all about changing the size of a shape. Imagine you have a tiny little Lego brick. A dilation could make it enormous, like a giant inflatable version, or it could shrink it down to a microscopic speck. The key here is that the shape itself doesn't get squished or stretched in weird ways; it just gets proportionally bigger or smaller.

Think of it like zooming in or out on a photo. When you zoom in, you're essentially dilating the image to make it larger. When you zoom out, you're dilating it to make it smaller. The aspect ratio, the proportions of the photo, stays the same, right? That's the essence of a dilation in geometry. The "scale factor" tells you how much it's getting bigger or smaller. A scale factor of 2 means it's doubling in size, while a scale factor of 0.5 means it's getting half as big.
Translations: The Smooth Slide
Translations are the simplest to grasp. They're all about moving a shape from one place to another without changing its orientation or size. Imagine you have a perfectly shaped cookie. A translation is like sliding that cookie across your plate. It’s still the same cookie, just in a new spot. No spinning, no resizing, just a straight-up slide.
Think about a conveyor belt. Items on a conveyor belt are constantly being translated. They move along, maintaining their shape and orientation. That's a perfect real-world example of a translation. You might hear terms like "vector" when talking about translations, which essentially just tells you the direction and distance of the slide. It’s like giving directions: "Go 3 steps east and 2 steps north."
Rotations: The Dizzy Dance
Rotations are where things get a bit more dynamic. They involve spinning a shape around a fixed point. Imagine a merry-go-round. The horses on the merry-go-round are rotating around the center. They're not sliding, and their size isn’t changing, but they are definitely spinning!

The "fixed point" is crucial here. It’s like the axle of a wheel. The shape spins around that point. You can spin it a little bit, or a lot. You can spin it clockwise or counter-clockwise. The amount you spin it is measured in degrees. So, a rotation of 90 degrees clockwise is a different move than a rotation of 180 degrees counter-clockwise. It’s like choosing how many steps your dancer takes around the stage.
Reflections: The Mirror Image Magic
Reflections are like looking in a mirror. They create a flipped image of a shape. Imagine you have a letter "F". If you hold a mirror up to it, you see a backward "F". That's a reflection! The original shape and its reflection are congruent (the same size and shape), but they are mirror images of each other.
The "line of reflection" is like the mirror itself. You can reflect a shape across a horizontal line, a vertical line, or even a diagonal line. It’s as if you’re folding the paper along that line, and the shape appears on the other side. Think about the wings of a butterfly – they are often reflections of each other. This is a beautiful natural example of how reflections work.
Why Are These Worksheets So Helpful?
Okay, so we’ve got the basic ideas. But why are these worksheets, with their answers, such a useful tool? Well, it’s all about practice and understanding.

When you’re working through a dilation problem on a worksheet, you might have to calculate new coordinates for the vertices of a shape after it’s been dilated by a certain scale factor. The answers show you if you got it right! This helps you build confidence and internalize the rules.
For translations, you’ll likely be adding or subtracting values to the coordinates to shift the shape. The worksheet answers confirm if you’ve moved it the correct distance and in the correct direction.
Rotations can be a bit trickier, involving some coordinate transformations that might seem a little abstract at first. But seeing the correct answers after you've attempted them can demystify the process. You start to see the patterns emerge.
And reflections? They’re about understanding how the coordinates change when you flip across an axis. The answers are your confirmation that you've accurately created that mirror image.

Ultimately, these worksheets are like mini-experiments. You get to apply the concepts you've learned, and the answers act as your feedback loop. They help you identify any lingering confusion and solidify your understanding. It’s not about memorizing formulas; it’s about developing an intuition for how shapes behave when they're moved, resized, spun, or flipped.
Beyond the Worksheet: Real-World Fun
Once you’re comfortable with these basic transformations, you’ll start seeing them everywhere. Architects use rotations and reflections to create symmetrical and visually appealing buildings. Graphic designers use dilations, translations, and rotations to create logos, advertisements, and website layouts. Game developers rely heavily on these concepts to make characters and environments feel dynamic and interactive.
Even simple things like folding a piece of paper to create a symmetrical design involve reflections. When you’re cutting out cookies, you might be creating shapes that are rotations or reflections of each other. It’s a fundamental language of visual design and spatial reasoning.
So, next time you encounter a geometry worksheet on dilations, translations, rotations, or reflections, don't just see it as homework. See it as an opportunity to play, to explore, and to unlock a deeper understanding of the world around you. And those answers? They’re not just solutions; they’re your stepping stones to becoming a geometry ninja!
