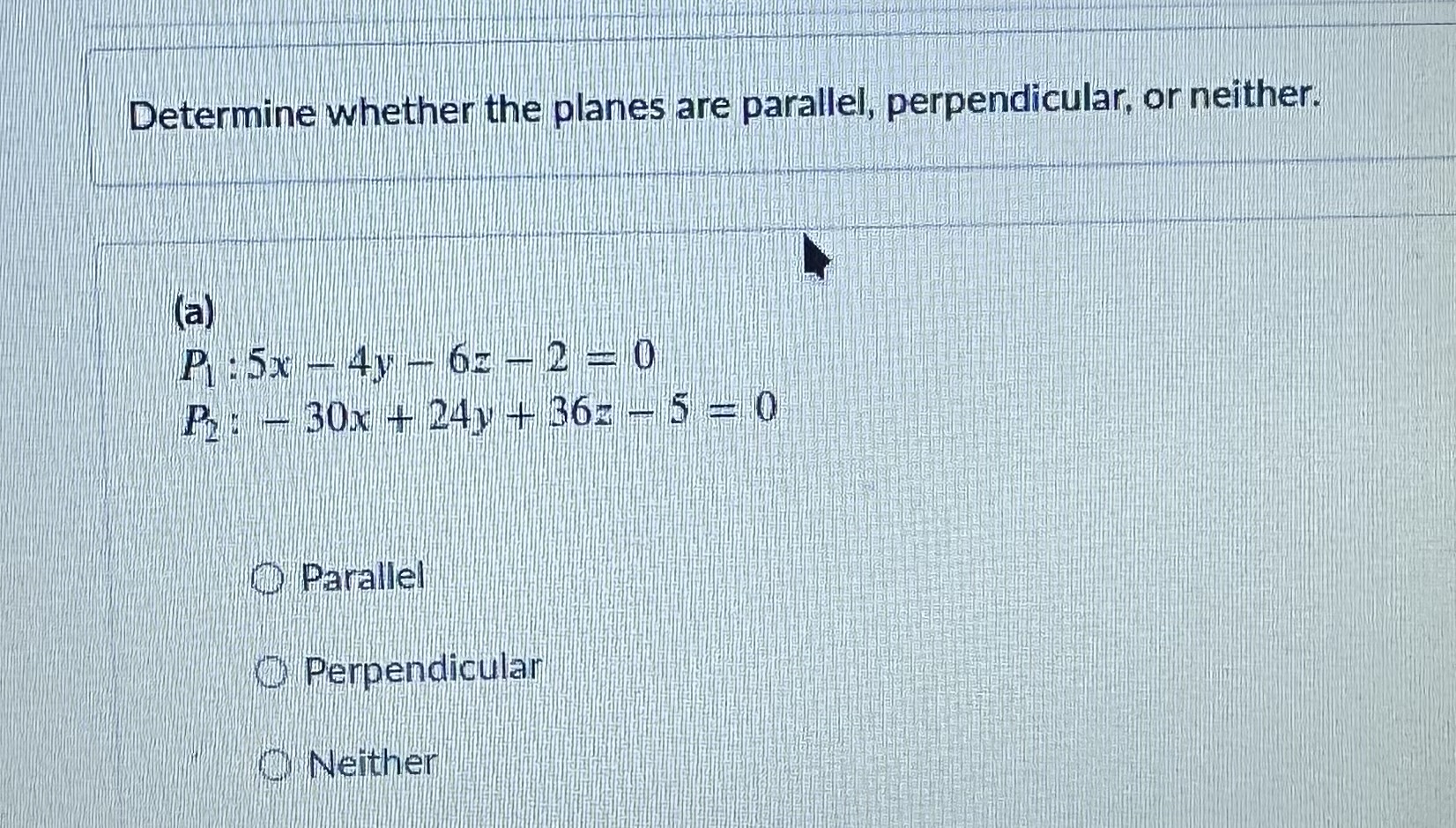
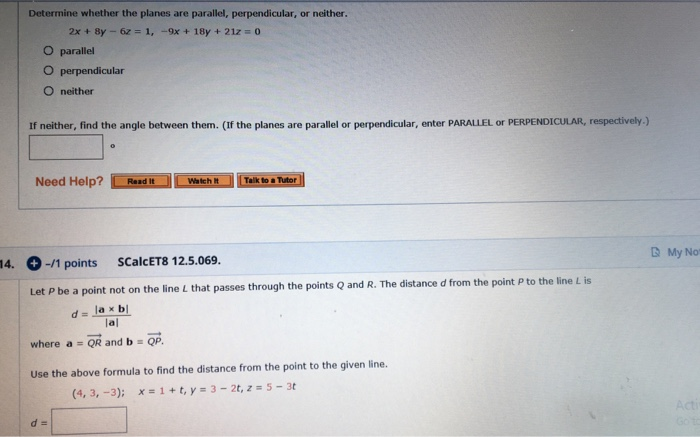
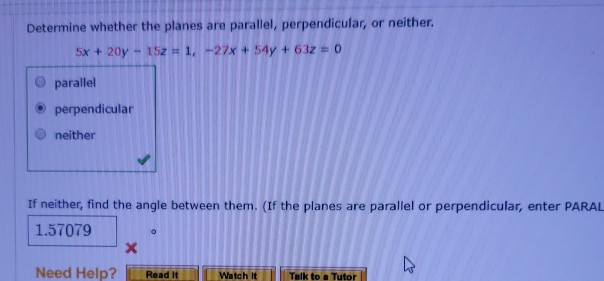
Determine Whether The Planes Are Parallel Perpendicular Or Neither
Hey there, future geometric gurus and spatial explorers! Ever looked up at the sky and wondered about the magnificent, invisible architecture that surrounds us? We're not talking about skyscrapers (though they're pretty cool too!), but the fascinating world of planes. And today, we're going to tackle a question that might sound a little bit intimidating, but trust me, it's going to be a blast: how do we figure out if planes are parallel, perpendicular, or just doing their own funky thing (a.k.a., neither!)?
Now, I know what you might be thinking. "Planes? Like airplanes?" Well, sort of! In math, a plane is basically a flat, endless surface. Think of a perfectly smooth tabletop that goes on forever, or the surface of a calm lake. It has length and width, but no thickness. And just like the real world, these mathematical planes can hang out in relation to each other in some pretty cool ways. It's like a cosmic dance, and we get to be the choreographers!
Why should you care, you ask? Oh, the reasons are endless! Understanding these spatial relationships can unlock a whole new way of seeing the world. It's like suddenly knowing the secret handshake to understanding how things fit together. It’s not just about math homework; it’s about appreciating the elegance of design in everything from a perfectly stacked brick wall to the vastness of the universe. And let's be honest, a little bit of mathematical swagger never hurt anyone, right?
The Parallel Pals: Friends Forever!
First up, let's talk about our parallel planes. Imagine two perfectly straight roads that stretch on and on, never, ever meeting. That's the essence of parallel planes! They are like two peas in a pod, existing side-by-side, always the same distance apart. They’ll never bump into each other, no matter how far they extend.
How do we spot these inseparable buddies? It all comes down to their normal vectors. Don't let that fancy word scare you! A normal vector is just a line that is perpendicular (we'll get to that!) to the plane itself. Think of it as a little flag sticking straight up out of our flat surface. If the normal vectors of two planes are pointing in the exact same direction (or the exact opposite direction, which is basically the same line!), then our planes are guaranteed to be parallel. It’s like they’re both flying in the same sky, on perfectly parallel flight paths!
So, the rule is simple: If the normal vectors are parallel, the planes are parallel. Easy peasy, lemon squeezy, right? This concept pops up everywhere. Think of the floor and ceiling of your room – they’re (ideally!) parallel. The pages of a book, stacked neatly – parallel! It’s a fundamental building block of our 3D world.

The Perpendicular Powerhouses: Meeting with Purpose!
Now, let's introduce another exciting relationship: perpendicular planes. These planes are like two best friends who meet at a perfect right angle. They don't just pass each other by; they intersect in a very specific, very orderly way. Think of a wall meeting the floor. That’s a classic example of perpendicularity!
How do we identify these purposeful meet-ups? Again, our trusty normal vectors come to the rescue! Remember those little flags? For perpendicular planes, the flags are going to be at a 90-degree angle to each other. They are essentially crossing paths at a perfect crossroads.
In mathematical terms, if the dot product of the normal vectors of two planes is zero, then the planes are perpendicular. Woah there, dot product! Don't panic. The dot product is just a way to multiply vectors that tells us about the angle between them. If it’s zero, it means they are at that magical 90-degree angle. It's like the universe saying, "Yup, these two are definitely shaking hands at a right angle!"
Perpendicular planes are everywhere too! Think of the sides of a box meeting each other. Or the shelves in a bookcase. They create structure and definition. They’re the workhorses of our built environment, ensuring everything stands up straight and in its proper place. It’s a beautiful kind of order, isn't it?
The "Neither" Noodlers: Doing Their Own Thing
And then, we have the vast majority of planes out there: the ones that are neither parallel nor perpendicular. These are the planes that are just… well, existing! They might intersect, but not at a right angle. They might be angled in some interesting way that doesn't align them perfectly parallel.
How do we know they fall into this category? It's actually pretty simple. If our planes don't meet the criteria for being parallel (their normal vectors aren't parallel) and they don't meet the criteria for being perpendicular (their normal vectors' dot product isn't zero), then congratulations! They are in the "neither" club. And that's perfectly okay!
This is where things get really interesting and, dare I say, a little more artistically inclined. Think of the slopes of a mountain range, or the tilted wings of an airplane. These are planes that are angled in countless ways, creating dynamic and beautiful shapes. They don’t adhere to strict rules of parallelism or perpendicularity, but they still define our world.
The beauty of the "neither" category is that it represents the incredible diversity and complexity of space. It's where true geometric exploration happens. It's like discovering a new nebula in the vastness of space – full of wonder and unexpected patterns.
Putting It All Together: Your Geometric Toolkit!
So, how do we actually do this? You’ll typically be given the equations of the planes. These equations will have coefficients that directly relate to those normal vectors we’ve been talking about. Let's say a plane is described by an equation like Ax + By + Cz = D. The numbers A, B, and C form the components of the normal vector!
To check for parallelism, you’ll compare the normal vectors of your two planes. Are the ratios of their corresponding components the same? If yes, they're parallel! To check for perpendicularity, you'll calculate the dot product of their normal vectors. If the result is zero, they're perpendicular!

If neither of these conditions is met, then you've got yourself a pair of "neither" planes. And that, my friends, is perfectly valid and incredibly common. It means you’re dealing with the beautiful, nuanced geometry of everyday life!
Learning to identify these relationships isn't just about acing a test (though that's a nice bonus!). It's about developing a deeper understanding of space, of how things align, and how they interact. It's a skill that can make you a better problem-solver, a more insightful observer, and just a generally more interesting person to chat with about the universe.
So, the next time you're looking at a building, a map, or even just the way your furniture is arranged, take a moment. Can you spot the parallel planes? The perpendicular intersections? Or perhaps, the elegantly angled "neither" planes? The world is a giant, fascinating geometric playground, and you now have a little more insight into its rules.
Don't stop here! This is just the tip of the iceberg. Dive deeper into the wonderful world of linear algebra and vector geometry. You'll be amazed at what you discover. You might even find yourself inspiring others to see the beauty in the mathematical structures that shape our reality. Go forth and explore, you magnificent geometry enthusiasts!
