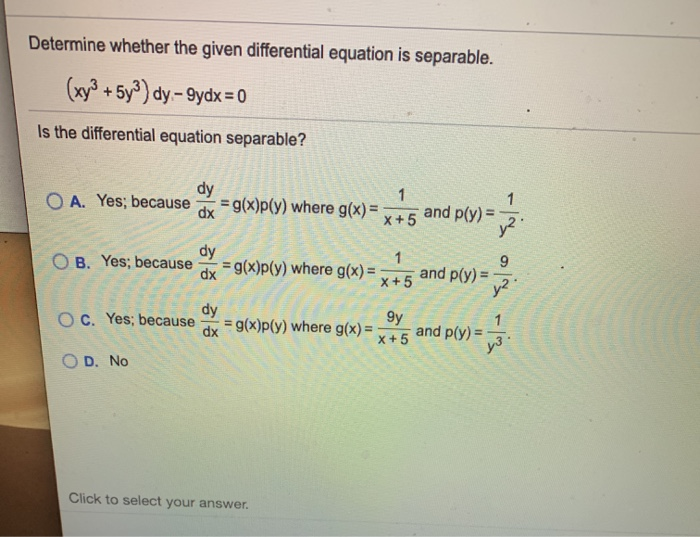
Determine Whether The Given Differential Equation Is Separable.
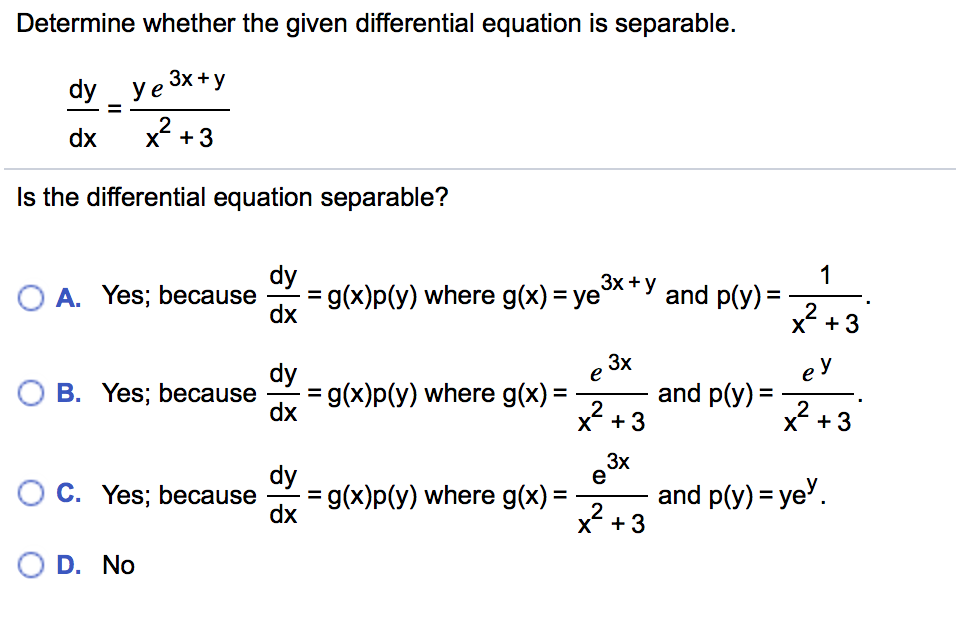
Imagine you've got a secret recipe for the most amazing cookies. It's a bit like a recipe, this math thing called a differential equation. It tells you how something changes, like how fast your cookie dough is spreading or how quickly the aroma fills your kitchen. Sometimes, these equations are a little shy, and we need to figure out if they're willing to be “separated.”
Think of it like this: you have two ingredients, let's call them x and y. A separable differential equation is like a recipe where you can neatly put all the x stuff in one bowl and all the y stuff in another, without them getting all mixed up too early. It's a bit like sorting your socks before laundry day – much easier to handle!
So, how do we know if our cookie recipe (or differential equation) is separable? It’s all about how the ingredients are presented. If you can arrange the recipe so that one side of the equation only has things related to x and its change (like dx), and the other side only has things related to y and its change (like dy), then congratulations! Your equation is separable.
The Tale of Two Variables
Let's meet our protagonists, x and y. They're often found in these equations, and their relationship is what we're trying to understand. Sometimes they’re best friends, and other times they’re like a quirky married couple, always influencing each other in complex ways.
When an equation is separable, it means x and y can have a moment alone. They can be treated independently for a little while. This makes solving the equation much, much easier. It’s like having a heart-to-heart with each of your friends before trying to solve a group problem.
The magic happens when we can write the equation in a special form. It looks something like f(x) dx = g(y) dy. See? All the xs are on one side, and all the ys are on the other. It’s a beautiful symmetry, a mathematical ballet of separation.

When Things Get Cozy (or Messy!)
Now, not all equations are this obliging. Sometimes, x and y are so intertwined, so deeply in love (or perhaps just stuck in a complicated situation), that you can’t pull them apart. Imagine trying to separate a perfectly blended smoothie – it’s not going to happen cleanly.
If you look at an equation and find that no matter how you rearrange it, you always have an x and a y bumping into each other on the same side, then it’s probably not separable. It’s like trying to separate two people who are holding hands very, very tightly. You might need a different approach, a more advanced technique.
This can feel a little disappointing at first, like finding out your favorite cookie recipe can’t be made with just half the ingredients. But don’t despair! It just means the problem requires a bit more finesse, a different kind of mathematical dance.
A Humorous Encounter
Let’s imagine a quirky scientist, Professor Quibble, who loves his equations like he loves his pet parrot, Archimedes. One day, Professor Quibble presents a new equation: ydx + xdy = 0. Archimedes squawks, "Separable! Separable!"
Professor Quibble, scratching his head, tries to move things around. He realizes he can write it as ydx = -xdy. Then, with a flourish, he divides both sides by xy, arriving at (1/x)dx = -(1/y)*dy. Archimedes does a little jig.
"Brilliant, my feathered friend!" exclaims Professor Quibble. "This one is indeed separable! We can integrate both sides independently and uncover the secrets of our changing universe!" It's a moment of triumph, a testament to the elegance of mathematical organization.
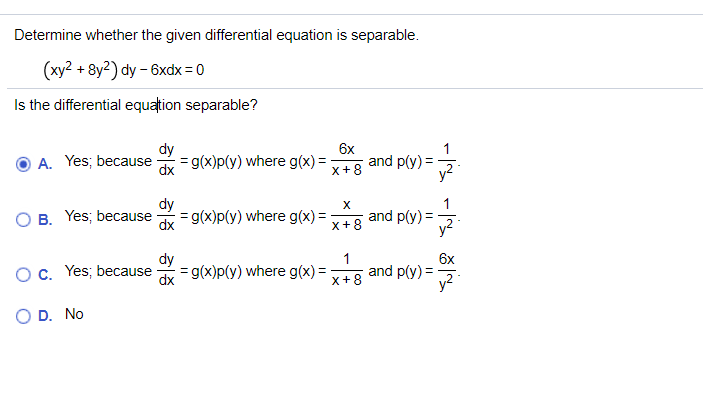
The Heartwarming Connection
Why do we even care if an equation is separable? Because it opens doors! It makes solving problems so much more accessible. It's like finding a shortcut on a long journey, a hidden path that leads you directly to your destination.
When an equation is separable, the integration step becomes a breeze. You integrate the x part, you integrate the y part, and voilà! You have a solution. It’s a moment of pure mathematical joy, like solving a puzzle that seemed impossibly complex at first.
This simplicity is heartwarming. It reminds us that even in the often intimidating world of mathematics, there are elegant solutions waiting to be discovered. It’s the beauty of breaking down a big, scary problem into smaller, manageable pieces.

Spotting the Separable Ones
So, the next time you encounter a differential equation, just ask yourself: can I get all the x-related terms with dx on one side, and all the y-related terms with dy on the other?
Look for multiplication or division that allows you to isolate the variables. If you see a function of x multiplied by dx and a function of y multiplied by dy, or things that can be easily rearranged into that form, you've likely found a separable treasure. It’s like spotting a perfectly organized bookshelf – a thing of beauty!
If it looks like a jumbled mess of xs and ys glued together, it might require a bit more advanced troubleshooting. But for those neat, separable equations, enjoy the ride. They’re a friendly introduction to the vast and fascinating world of differential equations, and they often lead to delightful discoveries.
