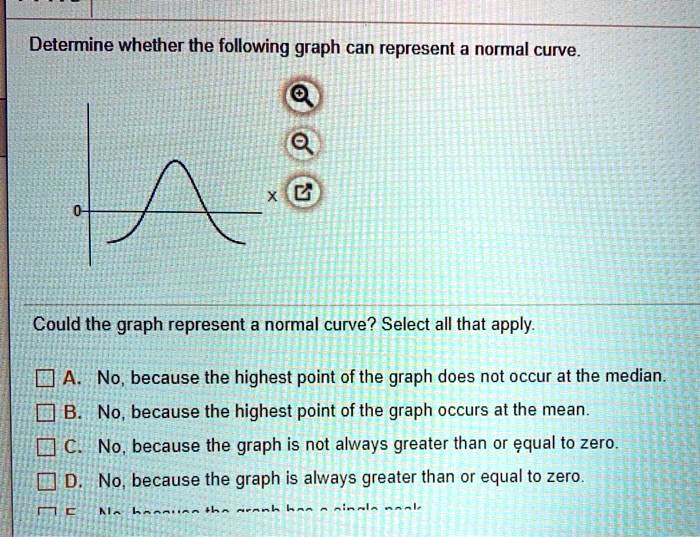
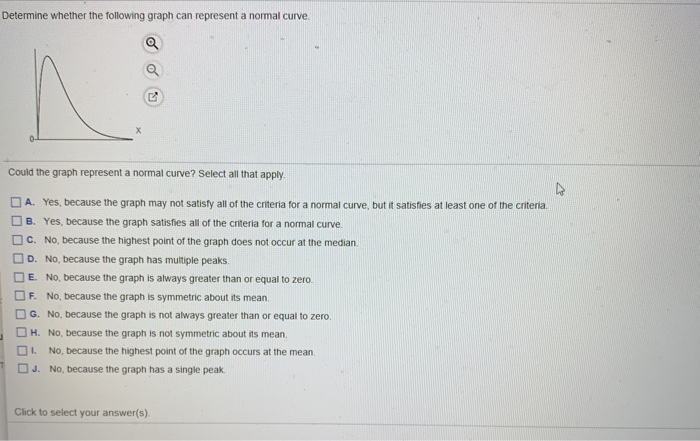
Determine Whether The Following Graph Can Represent A Normal Curve
Hey there, fellow humans! Ever looked at a bunch of data – maybe the heights of everyone in your family, the scores on a test, or even how many cookies you actually managed to resist eating on a given day – and wondered if it all follows some kind of predictable pattern? Today, we're going to chat about one of the most famous patterns out there: the normal curve. And more importantly, we’ll figure out if a graph you’re looking at could be this special bell-shaped beauty.
Think of the normal curve like the ultimate "average Joe" of data. It’s that classic bell shape you’ve probably seen somewhere, maybe on a statistics textbook cover or even in a quirky science documentary. It’s the shape that pops up when nature or human behavior decides to do its thing, and a lot of things in our world surprisingly fall into this pattern.
So, What's So Special About This Bell Shape?
Imagine you’re at a big party, and everyone is chatting. If you were to measure the exact decibel level of all the conversations happening at once, you’d probably find a few hushed whispers, a lot of normal chatter, and maybe a couple of really loud laugh-out-loud moments. If you plotted that, you’d likely get something that looks a lot like our normal curve. The most common sound level (the peak of the bell) would be the "normal" party chatter. The quieter sounds and the louder ones would be on either side, getting less and less frequent as you move away from the center.
This is the magic of the normal curve: most of the data points cluster around the middle (the average, the mean, the most common occurrence), and then they gradually taper off on both sides. It's like a perfectly symmetrical hill. On one side, you have the "less than usual" folks, and on the other, the "more than usual" folks. But the really, really extreme cases? They’re super rare, just like finding a unicorn at that party.
Why Should We Even Care About This Bell Thingy?
Honestly? Because it makes life a whole lot easier to understand! Think about it. If you know that something you're measuring tends to follow a normal curve, you can start to make some pretty smart guesses. For instance, if you're buying a product that's supposed to have a certain weight, and you know the weights are normally distributed, you can figure out what a "normal" range of weights is. If you get a package that feels suspiciously light or ridiculously heavy, you've got a good reason to raise an eyebrow (or maybe just call the company and ask for a replacement cookie if it's a cookie factory!).
It’s like understanding your car’s fuel gauge. You know that "full" is at the top, "empty" is at the bottom, and "half-full" is somewhere in the middle. The needle rarely just jumps randomly; it moves smoothly, reflecting the amount of fuel. The normal curve is like that for data – it gives us a framework to understand what's typical and what's an outlier.
Let's Look at a Graph: The Sherlock Holmes Edition
Now, the main event! You've got a graph in front of you. How do you tell if it's giving you the normal curve vibe? We're going to put on our detective hats and look for some key clues.
Clue #1: The Shape Itself – Is It a Bell?
This is the most obvious one. Does the graph have that distinctive bell shape? You should see a single peak right in the middle. This peak represents the mode (the most frequent value) and should be very close to the median (the middle value when all data is ordered) and the mean (the average). If your graph has two peaks, or looks like a lopsided mountain range, it's probably not a normal curve. Think of it like this: if you're sorting socks, and you have a pile of blue socks, a pile of red socks, and then a small pile of polka-dot socks, that's not a single, central peak. A normal curve is like having one giant pile of white socks, with just a few grey and black ones straggling on the edges.
So, check for that smooth, symmetrical curve. It shouldn't be flat, it shouldn't have sharp corners, and it definitely shouldn't be doing a jig on its own. Symmetry is key!
Clue #2: The Peak – Where's the Action?
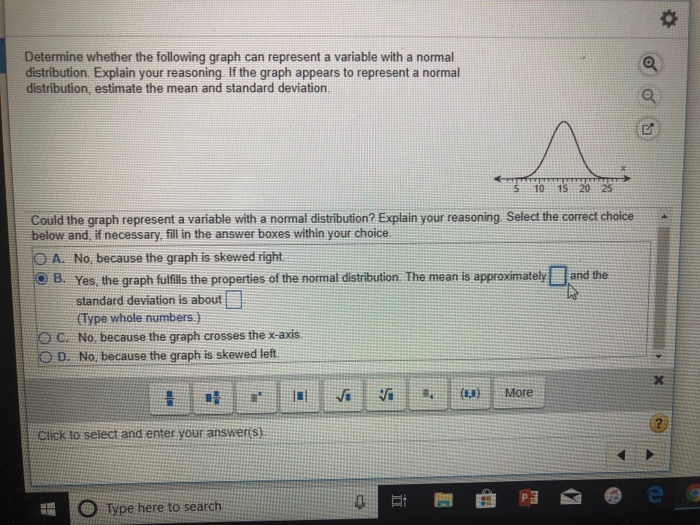
As we mentioned, the highest point of the curve, the peak, tells you where the most common data points are. In a perfect normal curve, this peak should be smack dab in the center. If the peak is way off to one side, the data is likely "skewed." Imagine a bunch of people lined up for ice cream. If the line is long and thin stretching way out to the right, most people are probably getting ice cream in the first few minutes (a right skew). If the line quickly gets short and there are only a few people at the very end, it might be a left skew. A normal curve means the line builds up evenly in the middle and then shrinks back down evenly on both sides.
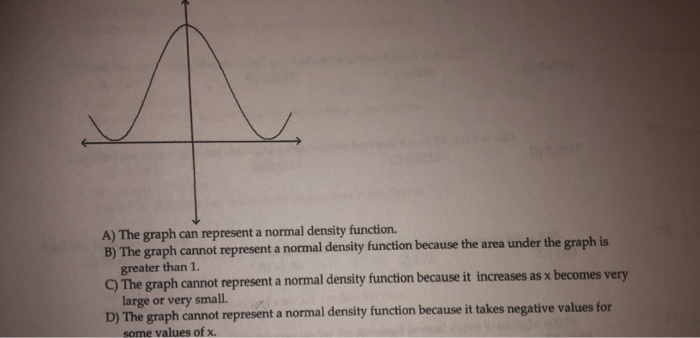
Clue #3: The Tails – Are They Gracefully Fading?
The "tails" are the parts of the graph that go off to the sides, away from the peak. In a normal curve, these tails should gradually get lower and lower as they move further away from the center. They should get closer and closer to the horizontal axis (the "zero" line) but never quite touch it. This means that extremely rare events can happen, but they are, well, extremely rare. If the tails drop off very suddenly, or if they seem to drag on forever, it might not be a normal distribution.
Think about your favorite song. Most people probably listen to it a lot. Some people listen to it occasionally. And then there’s that one superfan who plays it 24/7 – they're the extreme tail! But even they are a tiny fraction compared to the whole listener base. A normal curve accounts for those superfans, but they don’t dominate the picture.
Clue #4: The "Rule of 68-95-99.7" – A Little Cheat Sheet!
Okay, this one is a bit more technical, but it’s super helpful if you can find this information along with your graph. The normal curve has a predictable pattern for how the data spreads out from the center. It's often called the empirical rule or the 68-95-99.7 rule.
If you look at the data points that are one standard deviation (a measure of spread) away from the mean (the center): about 68% of your data should fall within that range.
If you look at data points that are two standard deviations away: about 95% of your data should be within that range.
And for data points that are three standard deviations away: about 99.7% of your data should be within that range. This means almost all of your data is within three standard deviations.
If you have a graph and you can see these percentages (or they are stated with the graph), and they’re close to these numbers, then congratulations! Your graph is giving you a big, happy nod towards being a normal curve. It’s like having a secret handshake with the data.

When It's NOT a Normal Curve
Sometimes, data just doesn't want to play by the bell-shaped rules. Maybe you're graphing the number of hours a superhero actually spends filing paperwork. That's probably going to be a very low number for most superheroes, with a few exceptions for the highly organized ones. This would likely be a skewed distribution, with a long tail towards higher numbers.
Or consider the heights of people only in a professional basketball league. You'd expect most people to be quite tall, with very few shorter individuals. That wouldn't be a nice, centered bell curve; it would be shifted heavily towards the "tall" end.
Putting It All Together
So, next time you see a graph and you’re wondering about its statistical personality, take a moment to look for these clues:
- Is it shaped like a symmetrical bell?
- Is the peak right in the middle?
- Do the tails fade gracefully?
- Do the 68-95-99.7 percentages roughly hold true?
If you answer "yes" to most of these, you're probably looking at a graph that can represent a normal curve. And that’s pretty neat! It means the world, in some mysterious way, is often acting predictably, even when it feels like chaos. It’s a little bit of order in the beautiful mess of life, all thanks to a charming, bell-shaped curve.
