Determine The Quadratic Function Whose Graph Is Given Below
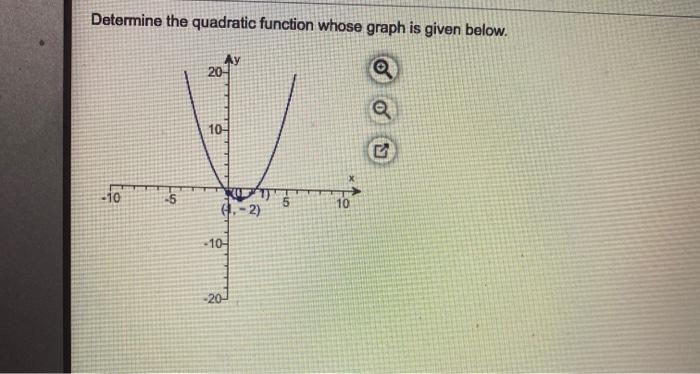
Alright, gather 'round, my math-curious comrades! Pull up a chair, grab a virtual croissant, and let's dive into the wild, wacky world of quadratic functions. You know, those parabolic beauties that look like they were drawn by a caffeinated squirrel on a rollercoaster. Today, we've got a special challenge: figuring out the exact equation of a quadratic function just by looking at its snazzy graph. Think of it like being a math detective, but instead of a magnifying glass, you've got your brain and a healthy dose of sass.
So, you're presented with this picture, right? It's a curve, doing its best impression of a smiley face or a grumpy frown, depending on which way it's facing. This, my friends, is our quadratic function's playground. And our mission, should we choose to accept it (and we totally should, because who doesn't love a good puzzle?), is to crack its code. We need to find that magical formula, the secret handshake, that brings this curve to life on paper.
Now, a quadratic function, for those of you who haven't had the pleasure, is basically a polynomial of degree two. That means the highest power of 'x' you'll find in its equation is a big, bold x². It looks something like y = ax² + bx + c. Don't let the 'a', 'b', and 'c' scare you; they're just fancy placeholders for numbers that will ultimately define the shape and position of our parabola. Think of them as the ingredients in a secret family recipe for a perfect parabola.
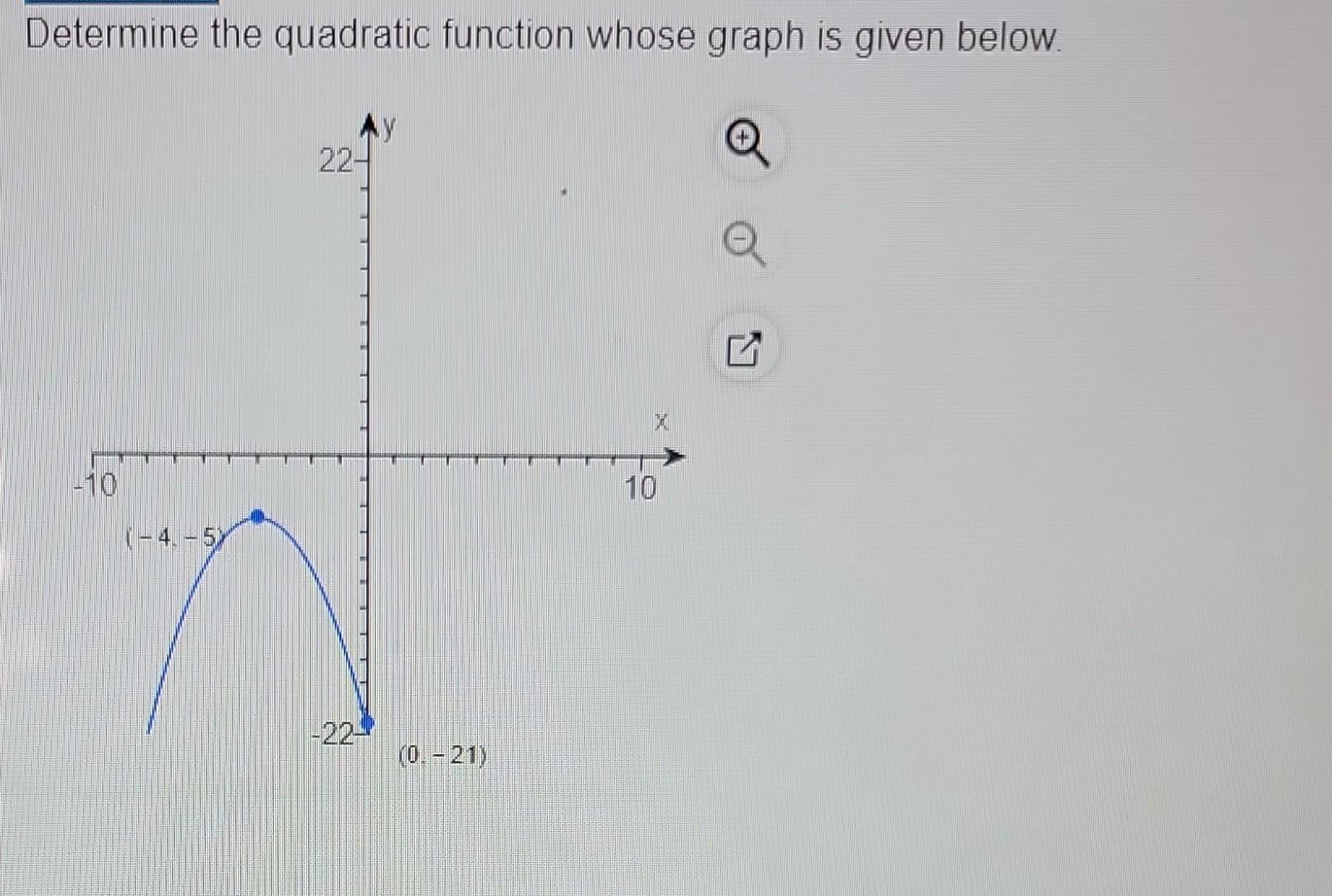
The first thing we need to do is eye this thing up. Where's the vertex? This is the tippy-top or the deepest dip of our parabola. It's like the peak of Mount Everest or the bottom of the Mariana Trench for our curve. This point is a treasure trove of information. Often, the vertex is conveniently placed at an easy-to-read coordinate, like (2, 5) or (-1, -3). If it's a nice, round number, your brain should start doing a happy little jig. If it's something like (√7, π/2), well, then you might need to take a deep breath and perhaps a stronger coffee. But hey, we’re detectives, not quitters!
Why is the vertex so important, you ask? Because it directly relates to the vertex form of a quadratic equation. This form is like a shortcut, a secret passage to finding our function. It looks like this: y = a(x - h)² + k. See those 'h' and 'k'? Yep, they're the coordinates of our vertex! So, if our vertex is at (h, k), we can immediately plug those numbers in. For instance, if the vertex is at (3, 1), our equation starts looking like y = a(x - 3)² + 1. Boom! Half the battle won, and we haven't even broken a sweat… yet.
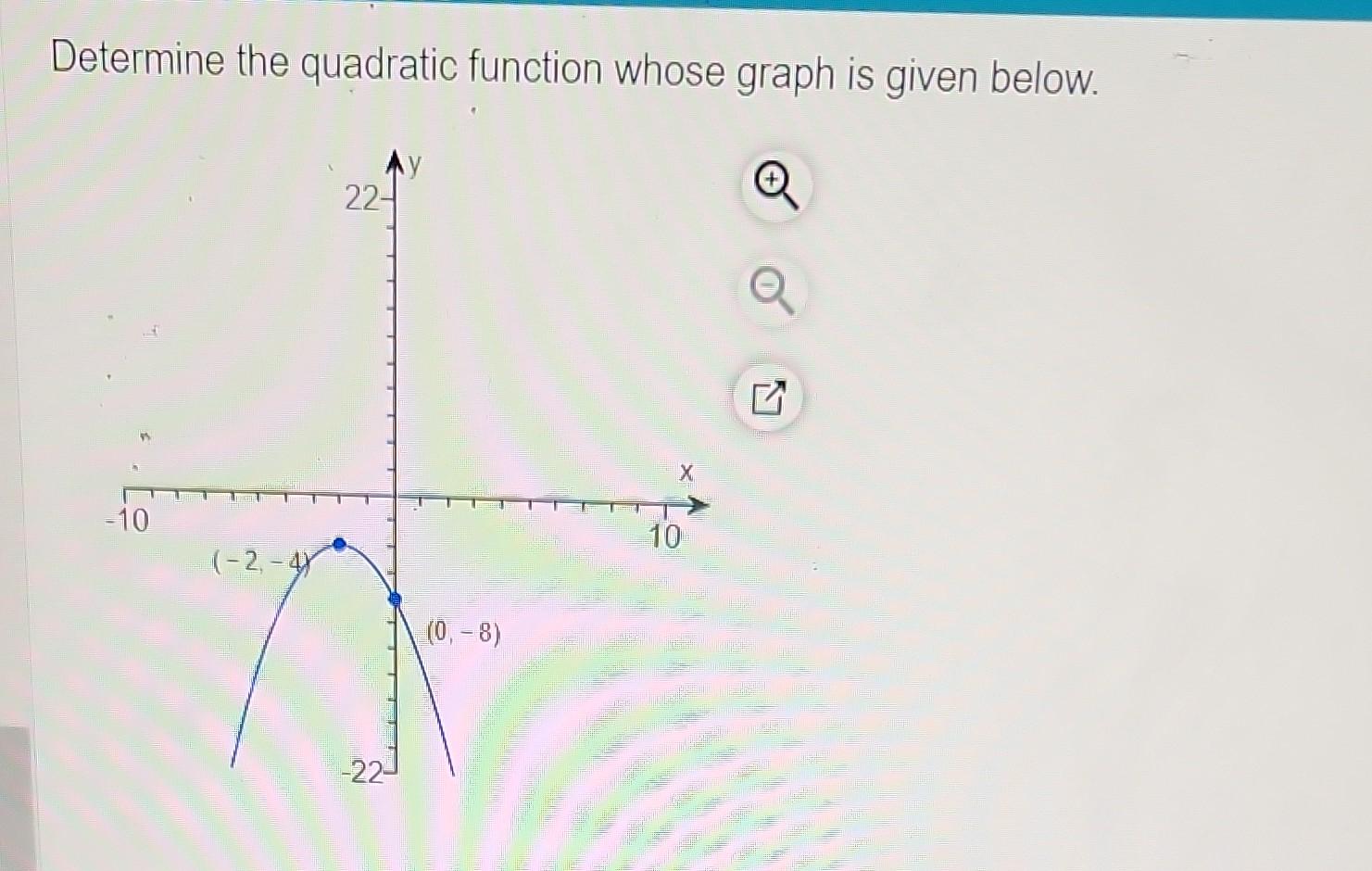
Now, we’ve got the 'h' and 'k' sorted, but what about the 'a'? This little guy is the superstar of stretch and direction. It determines whether our parabola opens upwards (like a cheerful sun) or downwards (like a perpetually unimpressed cat). A positive 'a' means it's smiling, and a negative 'a' means it's frowning. The bigger the absolute value of 'a', the skinnier our parabola; the smaller it is, the wider and more voluptuous it becomes. It’s like the zoom lens on a camera, but for math.
To find 'a', we need another piece of information. This is where we look for other points on the graph. Think of them as clues left by our parabolic criminal. The easiest points to find are usually the y-intercept (where the graph crosses the y-axis, which is always at x=0) or any other points with nice, whole number coordinates. Sometimes, the graph will be generous and even give you the x-intercepts (where it crosses the x-axis, meaning y=0). These are like finding a dropped wallet full of cash – pure gold!
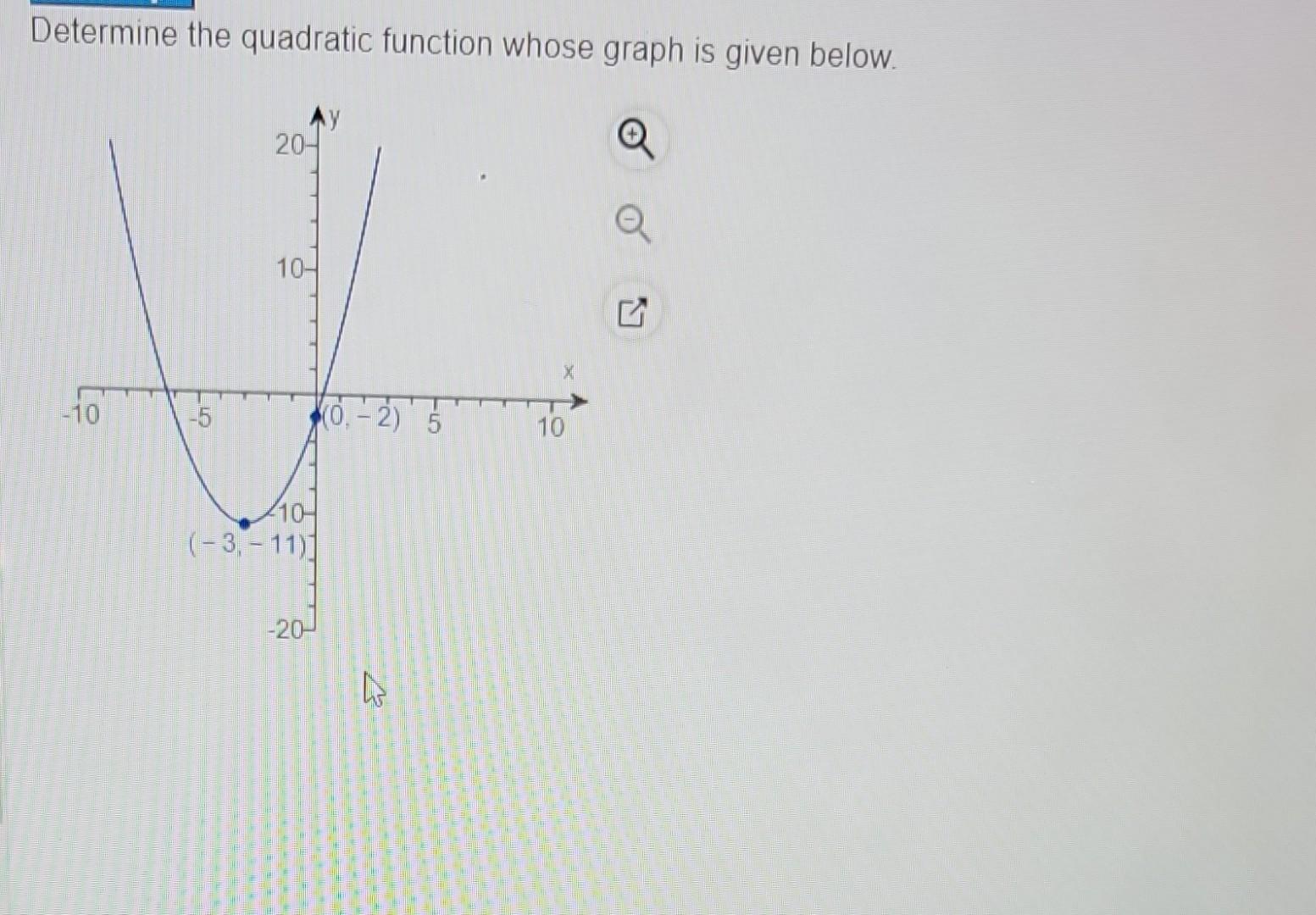
Let's say we found our vertex at (2, 5), so our equation is y = a(x - 2)² + 5. Now, we spot another point on the graph at (1, 7). This point, like all points on the graph, must satisfy the equation. So, we can substitute x=1 and y=7 into our equation: 7 = a(1 - 2)² + 5. Let's do some quick algebra, shall we? 7 = a(-1)² + 5. 7 = a(1) + 5. 7 = a + 5. Subtract 5 from both sides, and voilà! a = 2. Isn't that just delightful?
So, our full equation in vertex form is now y = 2(x - 2)² + 5. We did it! We cracked the code! You can practically hear the triumphant fanfare and the angels singing "Hallelujah!" (Or maybe that's just the coffee kicking in.)
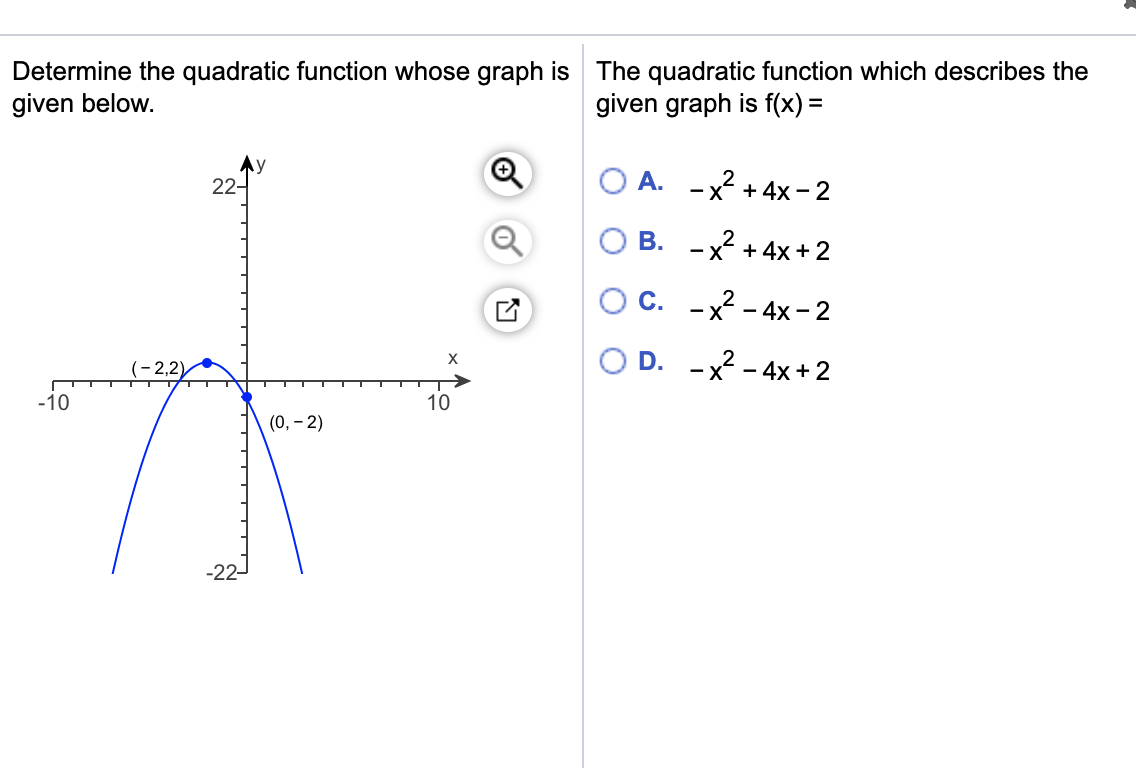
Sometimes, the question might ask for the equation in the standard form, y = ax² + bx + c. No worries, we can convert! We just need to do a little algebraic expansion. Remember that (x - 2)² is actually (x - 2)(x - 2). So, we distribute like we're handing out candy on Halloween: y = 2(x² - 2x - 2x + 4) + 5. Combine like terms: y = 2(x² - 4x + 4) + 5. Now, distribute that '2': y = 2x² - 8x + 8 + 5. And finally, combine the constants: y = 2x² - 8x + 13. Ta-da! Standard form, as requested!
Now, what if the vertex isn't so nicely placed? Or what if you're given three points instead of the vertex? Well, that's when we break out the factored form of a quadratic equation, which is y = a(x - r₁)(x - r₂), where r₁ and r₂ are the x-intercepts (or roots). If your graph has clear x-intercepts, this is your best friend. You plug in those intercepts, grab another point, and solve for 'a' just like we did before.
Or, if you're given three arbitrary points that aren't the vertex or x-intercepts, you can plug all three into the standard form y = ax² + bx + c. This will give you a system of three linear equations with three unknowns (a, b, and c). Solving systems of equations is a whole other adventure, but it's perfectly doable. It's like piecing together a jigsaw puzzle, but the pieces are numbers and equations. And the final picture is a beautiful, perfectly formed parabola!
The amazing thing about quadratic functions is their ubiquity. They're not just abstract math concepts; they describe the path of a thrown ball (ignoring air resistance, of course – physics is complicated!), the shape of satellite dishes, and even the trajectory of a rocket. So, the next time you see a parabolic arc, remember that you have the power to decode its mathematical DNA. You are, in essence, a parabola whisperer. How cool is that?
So, next time you’re presented with a graph that looks like it’s doing a graceful dive, don't be intimidated. Grab your virtual notepad, identify the vertex, find another point, and let the math magic unfold. You've got this! And remember, if all else fails, blame the coffee. It’s a classic move in the detective handbook.
