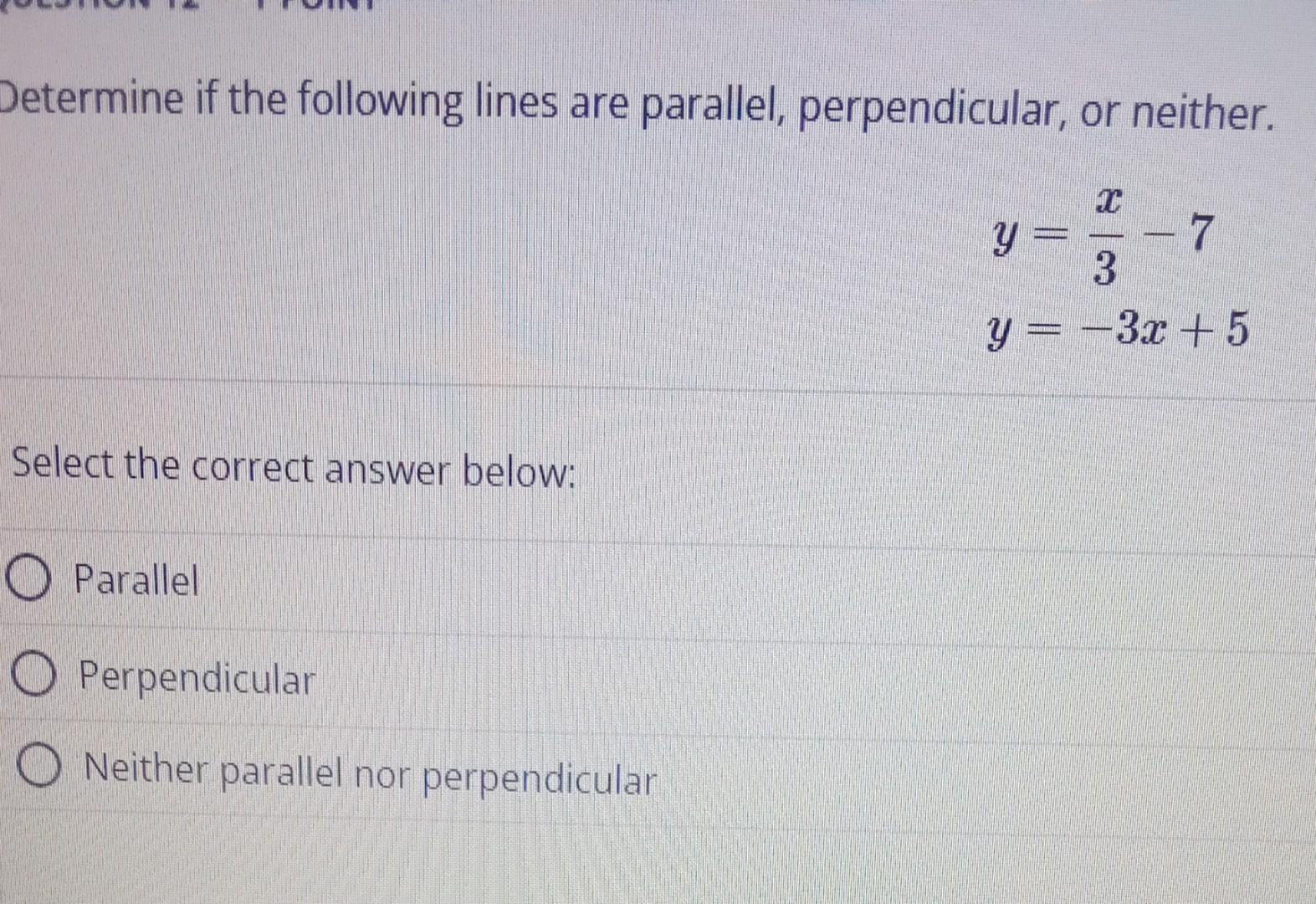
Determine If The Following Lines Are Parallel Perpendicular Or Neither

Hey there, fellow explorers of the world around us! Ever found yourself staring at something, maybe a couple of roads stretching out into the distance, or perhaps the way your curtains hang just so, and wondered… do these lines have a special relationship?
It might sound a bit academic, but figuring out if lines are parallel, perpendicular, or just hanging out, doing their own thing (that’s neither, by the way!), is actually a super useful skill. And the best part? It’s not as scary as it sounds. Think of it like understanding the unspoken rules of how things fit together in our everyday lives.
Let’s dive in, shall we? We’re going to break it down without any complicated jargon, just good old common sense and a few friendly examples.
The Art of Not Meeting: Parallel Lines
Imagine you’re on a train, looking out the window. The train tracks stretching out ahead of you, as far as the eye can see, are a perfect example of parallel lines. No matter how far you travel, those two rails will never touch. They’re like best friends who always walk side-by-side but never bump into each other.
Think about it::
- The edges of a perfectly rectangular picture frame.
- The lines on a lined notebook.
- Two lanes of a straight highway.
These lines are always the same distance apart. They’re the ultimate social distancers, but in a good, organized way. If you were to extend them forever, they’d still be cruising along, perfectly aligned, never crossing paths.
Mathematically, what makes them so chill? Well, in the world of graphs and equations, parallel lines have the exact same slope. The slope is basically the “steepness” or the “slant” of a line. If two lines have the same degree of slant, they’re going to stay on their own paths, parallel forever.
Why should you care about this? Well, understanding parallel lines helps us with design. Think about architecture. Buildings have straight, parallel lines everywhere to look stable and strong. Or even just hanging a picture frame straight on your wall – you’re subconsciously making sure the sides are parallel to the floor and ceiling!
The Perfect Crossing: Perpendicular Lines
Now, let’s switch gears to lines that do meet, but in a very specific, polite way. Think about a crisp “T” shape. The horizontal line and the vertical line meeting in the middle? Those are perpendicular lines. They meet at a perfect 90-degree angle, like a firm handshake or a neat corner of a room.

Picture this:
- The corner of a book.
- The intersection of a wall and the floor.
- The hands of a clock at 3 o’clock or 9 o’clock.
These lines are the opposite of parallel. Instead of giving each other space, they greet each other with a formal, right-angled embrace. They’re the ultimate organizers, creating neat, defined spaces.
In math-land, perpendicular lines have a special slope relationship. If one line has a slope of ‘m’, the perpendicular line will have a slope of ‘-1/m’. It’s like they have opposite personalities, but when they come together, they create perfect harmony. If one is going uphill steeply, the other is going downhill gently, ensuring they meet at that precise right angle.
This is super important for construction and engineering. Imagine building a house without perfectly perpendicular corners! It would be a wobbly mess. Roads need to intersect at right angles for traffic lights and clear intersections. Even something as simple as a door frame relies on perpendicular lines to function properly.
Just Doing Their Own Thing: Neither Parallel Nor Perpendicular
And then there are the lines that are just… there. They might cross each other at some point, but not at a neat 90-degree angle. Or they might be heading in different directions without any intention of meeting, but they also aren’t perfectly parallel. These are our neither lines.
Think about:

- Two friends walking in a park, each on their own meandering path.
- The way a river curves and flows, sometimes getting closer to another river but never becoming parallel or intersecting at a right angle.
- The criss-crossing branches of a tree.
These lines are the free spirits. They’re not bound by the strict rules of parallel or perpendicular. They might intersect, but it’s a casual, perhaps even accidental, meeting. They might run alongside each other for a bit, but their paths are destined to diverge or converge in a less structured way.
On a graph, this just means their slopes are different, and they don’t have that special inverse relationship needed for perpendicularity. They’re simply living their own lines, with their own unique slopes and directions.
Why care about ‘neither’? Because most things in life aren’t perfectly organized! Understanding this helps us appreciate the natural, organic flow of things. It’s about recognizing that not everything has to fit into neat boxes. It’s also important in fields like cartography (map-making) where coastlines and borders are rarely straight or perfectly aligned.
Putting It All Together: How Do We Tell?
So, how do we, as everyday detectives of lines, figure this out? The magic ingredient is usually the slope. If you’re given the equations of two lines, you just need to look at their slopes.
Let’s say you have two lines:
Line 1: y = 2x + 3
Line 2: y = 2x - 1

Look at the number in front of the ‘x’. In both equations, it’s a ‘2’. That’s the slope! Since the slopes are the same (both are 2), these lines are parallel. They’re like two identical twins, always walking at the same pace.
Now consider these:
Line A: y = 3x + 5
Line B: y = (-1/3)x + 2
The slope of Line A is 3. The slope of Line B is -1/3. Are they the same? Nope. But if you multiply them (3 * -1/3), you get -1. That’s our special rule for perpendicular lines! They meet at a perfect right angle.
And finally:
Line P: y = x + 4
Line Q: y = -2x + 1
The slopes are 1 and -2. They’re not the same, so they’re not parallel. If you multiply them (1 * -2), you get -2, which is not -1. So, they’re not perpendicular either. These lines are neither. They’ll cross eventually, but at a wonky angle.
Sometimes, you might be given points instead of equations. In that case, you’d calculate the slope using those points. The formula for slope is (change in y) / (change in x), or as we often say, "rise over run."
Why Does This Even Matter?
Beyond just acing a math quiz, understanding these relationships is like having a secret superpower for navigating the visual world. It helps us appreciate the order in chaos, the beauty in design, and the functionality in everyday objects.
When you see a perfectly laid brick wall, you’re seeing parallel and perpendicular lines working in harmony. When you’re using a map to navigate, you’re relying on the geometric relationships of the roads. Even when you’re just trying to hang a shelf evenly, you’re thinking about those angles!
So next time you’re out and about, take a moment to observe the lines around you. Are they parallel, cruising along like a peaceful train? Are they perpendicular, forming strong, stable corners? Or are they just doing their own thing, adding a touch of organic freedom to the world? It’s a simple observation, but it unlocks a deeper appreciation for the geometry that shapes our lives. Happy line-spotting!
