Determine Algebraically Whether The Function Is Even Odd Or Neither

Hey math enthusiasts and the delightfully curious! Ever found yourself staring at a function and wondering if it’s got a secret life – perhaps an even, odd, or maybe just a wonderfully neither personality? Unraveling the symmetry of functions, determining if they’re even, odd, or neither algebraically, is a bit like being a detective. It’s a satisfying mental puzzle that rewards you with a deeper understanding of how these mathematical relationships behave. Think of it as unlocking a hidden code, and the algebra is your trusty key!
Why bother with this mathematical sleuthing? Well, understanding function symmetry isn’t just for dusty textbooks. It has surprisingly practical applications. For instance, in physics, even functions often describe phenomena that are symmetrical with respect to a central point, like the potential energy in a simple harmonic oscillator. Odd functions, on the other hand, might represent quantities that change direction symmetrically, such as the electric field generated by a dipole. In engineering, recognizing these patterns can simplify complex calculations and predictions. Even in computer graphics, understanding symmetry can lead to more efficient algorithms for rendering shapes and animations. It’s all about spotting patterns that make life, and math, a little bit easier and more predictable.
So, how do we embark on this algebraic adventure? The process is surprisingly straightforward, yet profoundly insightful. To determine if a function $f(x)$ is even, you check if $f(-x) = f(x)$. This means that plugging in a negative value for $x$ gives you the exact same result as plugging in its positive counterpart. Imagine a mirror image on the y-axis – that's an even function! Think of $f(x) = x^2$ or $f(x) = \cos(x)$. They’re perfectly symmetrical around the y-axis.
Now, for odd functions, the test is slightly different. You’re looking for $f(-x) = -f(x)$. This implies a symmetry through the origin, like a rotation. If you reflect across the y-axis and then across the x-axis, you end up where you started. Classic examples include $f(x) = x^3$ or $f(x) = \sin(x)$. These functions have a rotational symmetry about the origin.
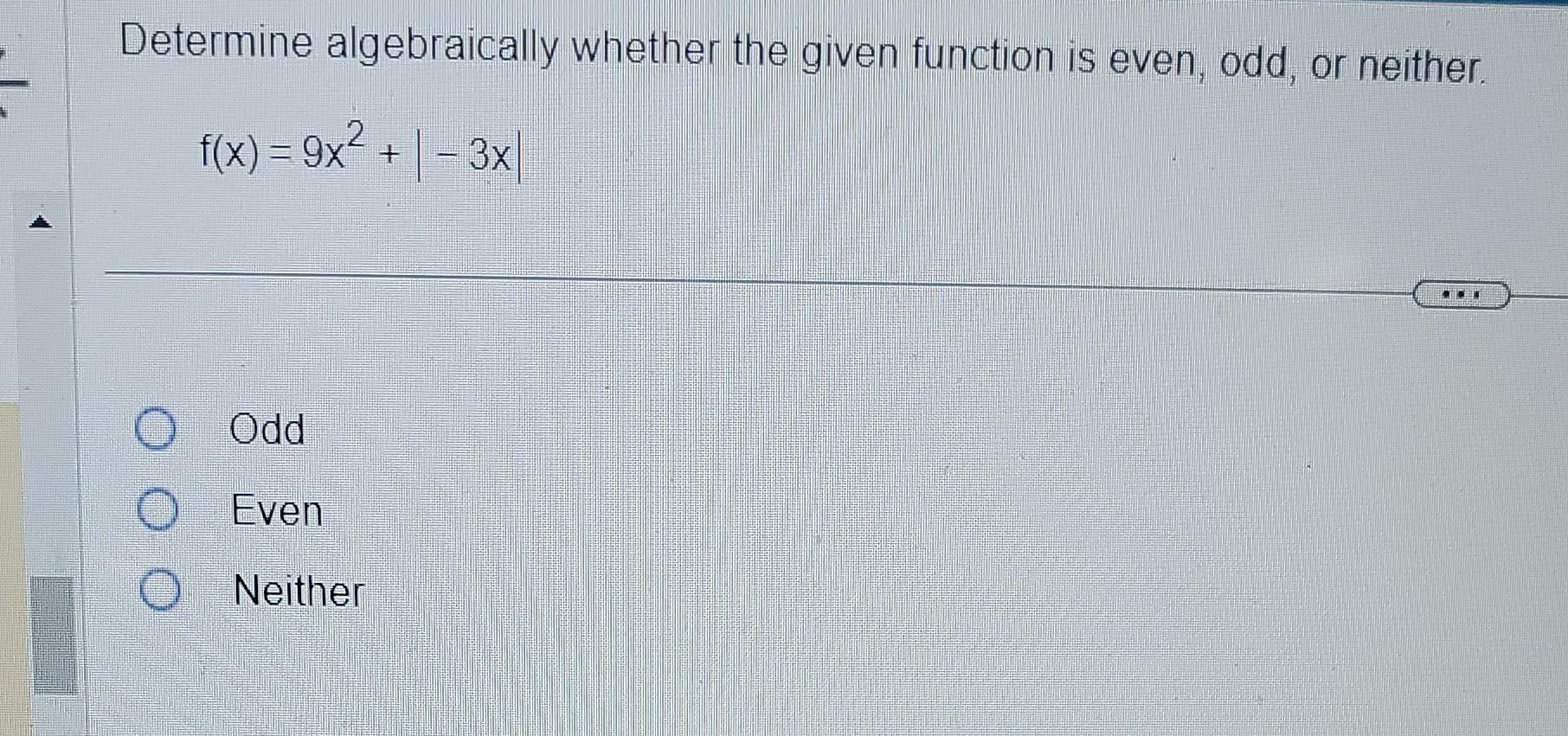
And what if neither of these conditions holds true? Then, my friends, your function is simply neither even nor odd. It might have some interesting properties, but it doesn’t fit neatly into these symmetrical categories. For example, $f(x) = x + 1$ is neither even nor odd.
To enjoy this process more effectively, here are a few practical tips. First, practice makes perfect. The more functions you analyze, the quicker you’ll become at spotting potential patterns. Second, visualize it. While the algebra is crucial, sketching a quick graph can give you an intuitive feel for the function’s symmetry, helping you confirm your algebraic findings. Third, don't be afraid of the algebra. Break down the $f(-x)$ substitution step-by-step. Simplify carefully, and if you get stuck, revisit the definitions. Embrace the challenge, and you’ll find a real sense of accomplishment in mastering this fundamental aspect of function analysis!
