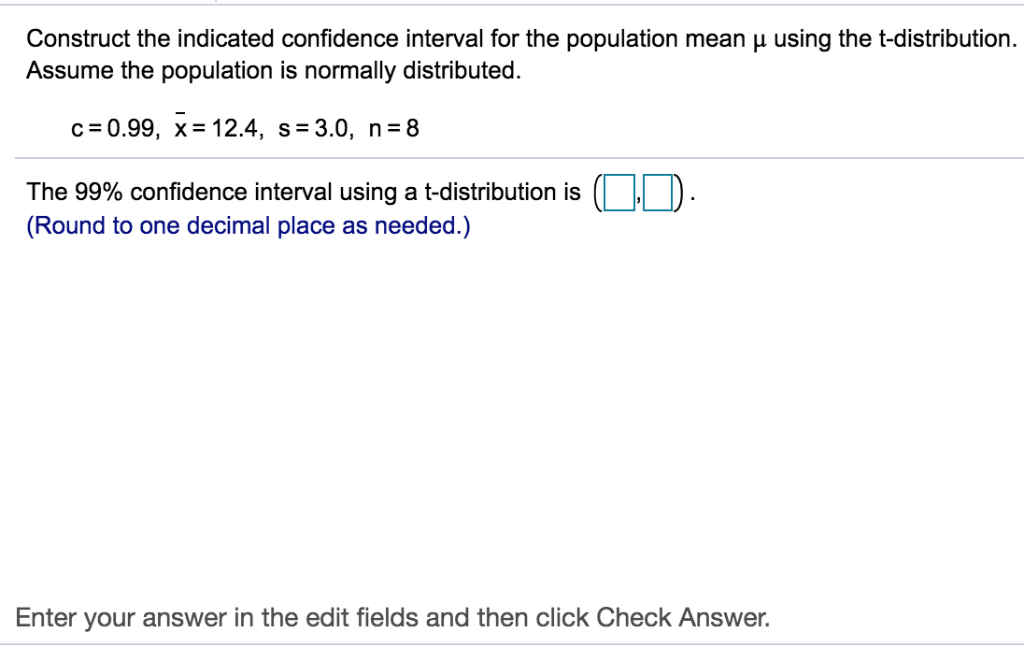
Construct The Indicated Confidence Interval For The Population Mean

Hey there, curious minds and data explorers! Ever wondered how we can make educated guesses about big groups of people (or things!) without actually talking to every single one of them? It’s like trying to figure out the average height of all the people in your city without measuring them all. Sounds tricky, right? Well, get ready to have your mind gently blown, because we're diving into the wonderful world of confidence intervals for the population mean!
Now, I know what you might be thinking: "Confidence interval? Sounds a bit… mathy. Is this going to be one of those dry, textbook things?" Nope, nope, and a big fat nope! We're going to keep this light, breezy, and, dare I say, fun. Think of it as a superpower you're about to unlock – a superpower to make smart predictions and feel super confident about them, even when you don't have all the answers.
So, What's the Big Idea Anyway?
Imagine you're a baker, and you want to know the average number of sprinkles people really want on their cookies. You can't ask everyone in the world, can you? That would be a LOT of cookies. So, you take a sample – maybe you ask 100 people at a local bake sale.
From your sample, you calculate the average number of sprinkles. Let's say it’s 25. Great! But is that exactly the average for everyone? Probably not. It’s super unlikely that your small group of 100 people perfectly represents the entire planet’s sprinkle preferences.
This is where our hero, the confidence interval, swoops in! Instead of just giving you a single number (25 sprinkles), a confidence interval gives you a range of numbers. It's like saying, "Okay, based on my sample, I'm pretty sure the true average number of sprinkles people want is somewhere between 20 and 30." See? Much more realistic and honest!
What Does "Confidence" Even Mean Here?
This is the really cool part, and it’s often misunderstood. When we say "95% confidence interval," we’re not saying there’s a 95% chance the true average falls within this specific range we calculated. That’s a common misconception!
Instead, it means that if we were to repeat this process many, many times – taking 100-person samples, calculating an interval each time – then about 95% of those intervals would contain the true population average. Think of it like a consistent net, cast out again and again. Most of the time, it catches the fish (the true average).
So, it’s about the reliability of the method, not the probability of a specific result. And that, my friends, is a subtle but powerful distinction! It gives us a level of trust in our findings.
Why Should You Care About This Funky Interval?
Okay, sprinkles are fun, but let's think about real-world applications. Imagine you're a scientist studying the average blood pressure of a certain group of people. Or a business owner trying to estimate the average spending of your online customers. Or even a town planner trying to figure out the average commute time for residents.
In all these scenarios, we can't possibly survey everyone. But we can take a representative sample. And by constructing a confidence interval, we can make an educated guess about the true population value with a certain level of confidence. This is huge!
It helps us make better decisions. If a business wants to know if their new marketing campaign is increasing average customer spending, they can look at the confidence interval. If the interval for spending after the campaign is significantly higher than the interval before, they have strong evidence that their campaign is working!

It also helps us understand uncertainty. Life is rarely black and white, and statistics should reflect that. A confidence interval acknowledges that there’s a bit of wiggle room in our estimates. It’s like saying, "This is my best guess, and here's the reasonable range of what it could truly be." That's honest and incredibly useful!
Building Your Own Confidence Interval (Don't Worry, It's Not Scary!)
So, how do we actually build one of these magical intervals? It’s not as complicated as it sounds, especially when you have a calculator or software to help. The basic idea involves three key ingredients:
1. The Sample Mean: This is your best single guess from your collected data. (Remember our 25 sprinkles?) 2. The Margin of Error: This is how much "wiggle room" you’re adding to your guess. It's calculated based on how spread out your data is and how confident you want to be. 3. The Confidence Level: This is usually expressed as a percentage (like 90%, 95%, or 99%). The higher the confidence level, the wider your interval will be. You're trading precision for certainty. It's a classic trade-off, isn't it?
The formula generally looks something like: Sample Mean ± Margin of Error.

The margin of error itself is usually calculated using something called the standard error (which measures how much the sample mean is likely to vary from the true population mean) and a value from a special distribution (like the z-distribution or t-distribution, depending on your sample size and whether you know the population standard deviation – but don't let those names scare you!).
Think of the standard error as the "stickiness" of your sample. If your sample data is all over the place, your standard error will be higher, leading to a wider interval. If your sample is very consistent, your standard error will be lower, and your interval will be narrower.
Let's Get Practical!
Imagine you're analyzing the average time it takes for your new software to load. You test it 30 times and find the average load time is 3.5 seconds, with a certain amount of variation. You decide you want a 95% confidence interval.
Using statistical software or a handy calculator, you plug in your sample mean, the sample standard deviation, and your desired confidence level. Voila! You might get an interval like (3.2 seconds, 3.8 seconds). This tells you that you’re 95% confident that the true average load time for your software across all possible loads is somewhere between 3.2 and 3.8 seconds.

This is super helpful! If your target was to have an average load time under 3 seconds, you can now see that your current performance, while averaging 3.5 seconds, has a lower bound of 3.2 seconds. That gives you a clear indication that you’re not hitting your target consistently. And you know this without testing millions of loads!
Making Life More Fun with Confidence Intervals!
Honestly, understanding confidence intervals can inject a little bit of statistical swagger into your life. When you see news reports about poll results or scientific studies, you’ll be able to mentally (or even explicitly!) add that layer of understanding about the margin of error and confidence level. You’ll be a more critical and informed consumer of information.
It’s also a fantastic way to approach everyday questions. Wondering about the average price of a decent cup of coffee in your neighborhood? Want to estimate the average number of steps you take on a typical weekday? You can take a few samples, do some quick calculations (or use an app!), and come up with a confidence interval. It’s like having a personal data detective at your service!
This journey into confidence intervals is all about transforming raw data into meaningful insights. It's about moving beyond just a single number and embracing the nuance of estimation. It's about making smarter, more informed decisions with a comfortable level of certainty.
So, go forth and explore! Don't be afraid of a little math. Embrace the power of the confidence interval. It’s a tool that can demystify the world around you, one estimated mean at a time. You’ve got this, and the world of data is waiting for your curious spirit!
