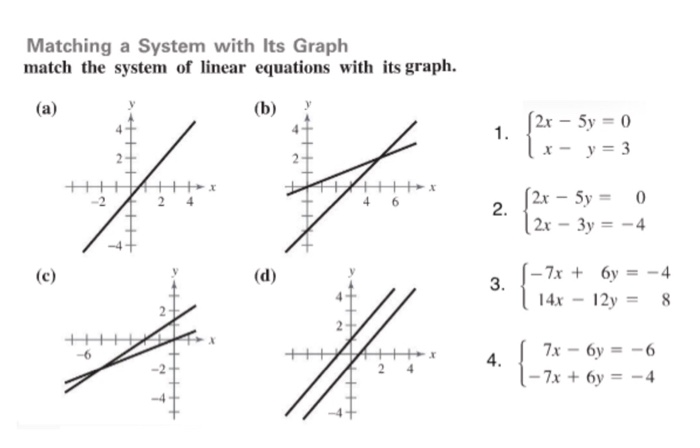
Choose The System Of Equations That Matches The Following Graph

Imagine you're at a quirky art gallery opening, and on the wall is this absolutely wild piece of art. It's not a painting, not a sculpture, but a dazzling display of intersecting lines, all sorts of colors and angles. It looks like a secret map to a treasure chest, or maybe the blueprint for a truly spectacular, if slightly chaotic, roller coaster.
Now, the artist, let's call her Esmeralda "Sparkle" Jenson, has left a little note next to it. It's not a description, oh no, that would be too easy! Instead, she's presented you with a few options, a multiple-choice test for your inner detective. Each option is a "system of equations," which sounds fancy, but think of it like a secret handshake or a special recipe.
Your mission, should you choose to accept it (and trust us, it's a fun one!), is to figure out which of Esmeralda's secret recipes perfectly describes the beautiful, messy lines you see on the wall. It's like trying to match a love letter to its author, or a delicious cookie recipe to the cookie itself.
Let's peek at one of these "systems of equations." It might look like this:
Equation 1: x + y = 5
Equation 2: 2x - y = 1
Now, this isn't some scary math homework. Think of 'x' and 'y' as little secret codes. When you have an equation like x + y = 5, it's like saying, "The secret number 'x' plus the secret number 'y' always adds up to 5." It's like two friends, each with a certain number of candies, and together they have exactly 5.
And then there's the second equation, 2x - y = 1. This one is like a different rule for the same two friends. It's saying, "If you take twice the number of candies 'x' has, and then take away the number 'y' has, you'll end up with 1 candy." It’s a bit more complicated, like a secret game they play with their candies.
So, when we see these lines on Esmeralda's artwork, each line represents one of these secret recipes, or equations. The place where the lines cross, that's the magical spot where both secret recipes are true at the same time! It's the only point where the two friends can agree on the numbers of candies they have, fulfilling both their candy-sharing rules.

Finding that intersection point is like finding the pot of gold at the end of the rainbow. It’s the answer, the solution, the key to unlocking Esmeralda’s artistic puzzle. And the system of equations that matches the graph is simply the set of rules (the equations) that created those specific lines and their crossing point.
Think about it like this: You're trying to find your best friend in a bustling market. You have two clues: 1) They promised to meet you near the big, red apple stand. 2) They said they'd be wearing their bright yellow hat. The place where you see someone at the red apple stand and wearing a yellow hat – that's your intersection point! The clues are your "system of equations."
Sometimes, the lines might be perfectly straight, like a freshly ruled piece of paper. Other times, they might be a little wiggly, like a happy dog's tail wagging. The "system of equations" tells you what kind of lines you're going to get.
If you have equations with just 'x' and 'y' raised to the power of 1 (like we saw above), you get those lovely straight lines. These are called linear equations, and they're like the reliable, always-there-for-you kind of friends. They keep things simple and predictable.
But what if one of the equations has an 'x' or 'y' squared (like x² or y²)? Suddenly, you're not dealing with straight lines anymore! You might get beautiful curves, circles, or even those dramatic parabolas that look like smiling mouths or sad frowns. These are like the more exciting, unpredictable friends who bring a bit of flair to the party.
When you're looking at Esmeralda's artwork, you're essentially decoding her artistic language. You're seeing the visual representation of mathematical relationships. The graph is the story, and the system of equations is the narrative that tells it.
So, how do you actually pick the right system? It's a bit like being a fashion critic. You look at the outfit (the graph) and then you check the designer's label (the systems of equations). Does the style match?
First, check the slopes. Does the line go uphill from left to right, or downhill? Is it steep, or does it take its sweet time? Each equation has a "slope" that dictates this. A positive slope means uphill, a negative slope means downhill.
Then, look at the y-intercept. This is where the line crosses the vertical y-axis. Does it cross high up, low down, or right at the origin (the center point)? Each equation also tells you where its line will kiss the y-axis.
If your graph has curves, you'll be looking for those squared terms in the equations. A term like x² often leads to curves. The more complex the curve, the more complex the equations that made it.
And the most important clue of all? The intersection point! This is the 'aha!' moment. You need to find the system of equations where the solution (the values of 'x' and 'y' that make all the equations true) is the exact coordinate of that crossing point on your graph.
It's like finding the perfect key for a lock. You try a key, and if it fits perfectly and opens the door, you know it's the right one. Here, you substitute the coordinates of the intersection point into each equation in a system. If all the equations ring true, voilà! You've found your match.
Sometimes, the intersection point might be a neat, whole number, like (2, 3). This makes things a bit easier, like finding a perfectly ripe strawberry. Other times, it might be a decimal or a fraction, like (1.75, 3.25). These are like slightly more exotic fruits, still delicious, just require a bit more precision.
Esmeralda might have a system that looks like this:
Equation A: y = x + 1
Equation B: y = -2x + 4Choose the graph that matches the following system of equations: 5x
If you look at your graph and see two lines crossing at the point where x is 1 and y is 2, you can test this system. For Equation A: Is 2 equal to 1 + 1? Yes! For Equation B: Is 2 equal to -2(1) + 4? Yes! Since both are true, this is the winning system for that particular graph. It’s the secret recipe that baked the cookie you’re admiring.
The beauty of this is that math, which can sometimes feel a bit intimidating, becomes a language for describing the world around us, even in art. These systems of equations are just tools, like paintbrushes or chisels, that artists and mathematicians use to create and understand.
So, the next time you see a graph that looks like a beautiful, intricate drawing, don't be shy! Think of it as a puzzle from Esmeralda Jenson, and the systems of equations are your clues. It's a delightful dance between algebra and art, a secret handshake between numbers and shapes, and you're invited to join the fun!
It’s not about memorizing formulas, it's about seeing the connections. It's about understanding how these abstract ideas can represent something tangible and, dare we say, even beautiful. It's a little bit like solving a mystery, with the graph as the crime scene and the system of equations as the detective's notebook.
And the most heartwarming part? These seemingly complex concepts are built on simple, logical relationships. It’s the mathematical equivalent of a comforting hug, assuring us that even in complexity, there’s order and elegance to be found. So go forth, and find the system that sings the song of your graph!

