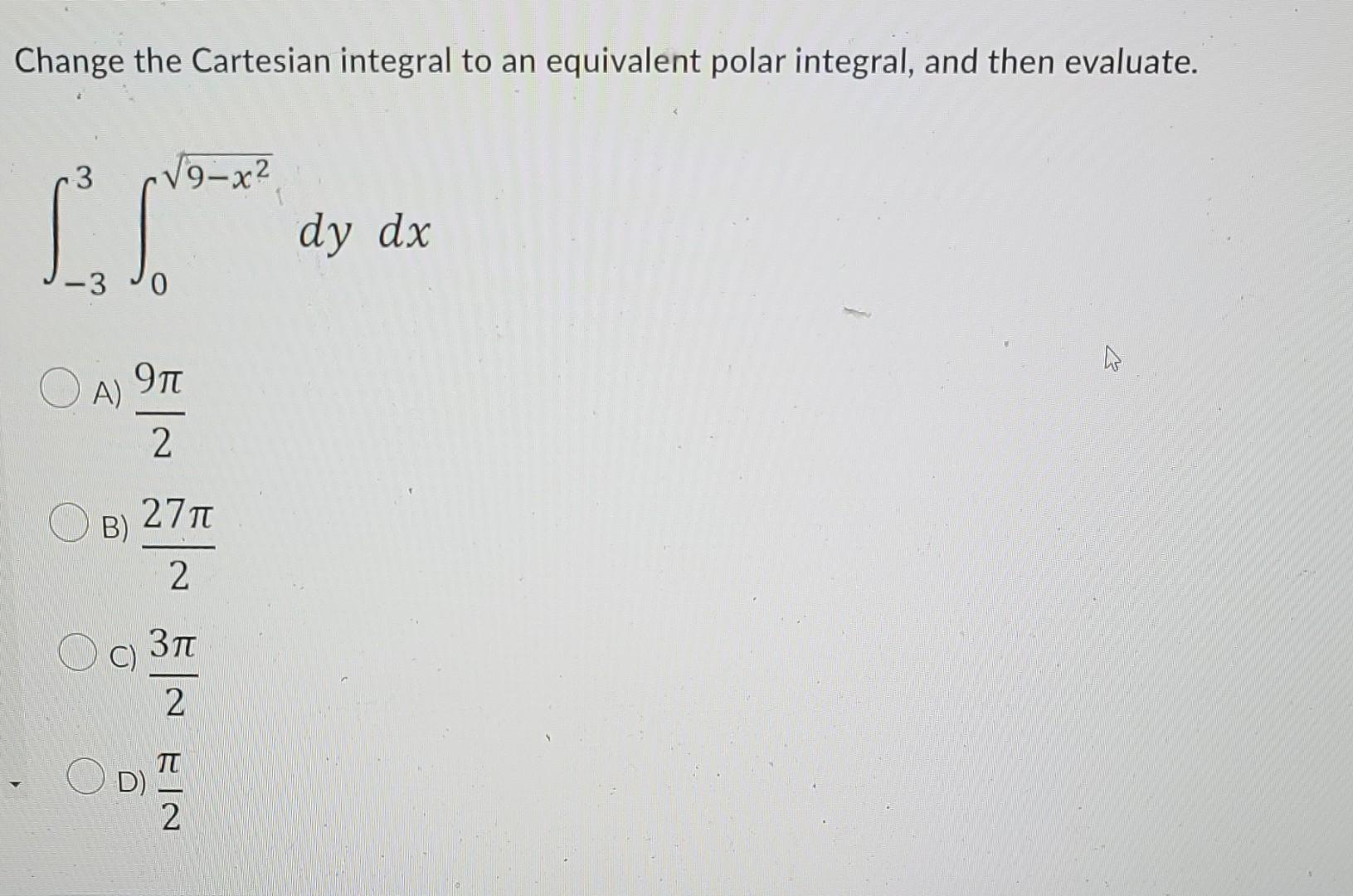
Change The Cartesian Integral Into An Equivalent Polar Integral

Hey there, math explorer! Ever looked at an integral and thought, "Man, this looks like a job"?
Well, sometimes it is! Especially when things get a bit… square. But what if I told you there's a secret handshake? A magical transformation that can make even the grumpiest integral smile?
We're talking about a little something called changing a Cartesian integral into a polar integral. Sounds fancy, right? But it's actually super cool. Like discovering a cheat code for your math homework.
Think of it like this: you're trying to describe a donut. In plain old Cartesian coordinates (you know, the x and y stuff), it’s all straight lines and right angles. Kinda… stiff.
But a donut is round! It's curvy! It's *polar!
So, instead of trying to cram that glorious roundness into a boxy grid, we whip out our polar coordinates. It's like trading your sensible walking shoes for a pair of dancing slippers. Suddenly, everything feels a bit more… free-flowing.
Why would you even bother? Great question! Sometimes, an integral that looks like a grumpy bear in Cartesian land becomes a happy little puppy in polar land. It’s all about finding the right perspective.
Imagine trying to measure the area of a perfectly circular pizza. In Cartesian, you’d be dealing with complicated curves and probably a lot of tricky square roots. No fun.
But in polar coordinates? Boom! It’s just a circle. Easy peasy. The math just sings.
So, how does this magic happen? It’s all about a little switcheroo.
The Big Reveal: x, y, and the Polar Pals
You know those trusty x and y variables? They’re like the classic duo, always there for you. But in polar land, they have new best friends: r and θ (that’s ‘theta’, by the way).
r is your distance from the center. Think of it as the radius of your circle.
θ is your angle. Imagine spinning around from a starting point. That’s your theta.
And here’s the secret sauce:
x = r cos(θ)
y = r sin(θ)
It’s like a secret code! You can always translate between the two worlds.
And for the integral itself? We get another little friend: dA. In Cartesian, dA is just dx dy (or dy dx, depending on your mood).
But in polar? It becomes r dr dθ. That ‘r’ is important! Don't forget it. It’s the secret handshake that makes the polar integral work its magic. It’s like the ingredient that makes the cookies taste extra good.
When Does This Polar Party Start?
Okay, so when is it time to ditch the squares and embrace the circles?

Look for regions that are round. Seriously. If your area of interest looks like a circle, a part of a circle, or anything with a nice, swooshy curve, polar coordinates are your jam.
Think about:
- Circles, obviously!
- Annuli (that’s a fancy word for a donut shape, or two circles with different radii).
- Regions described by angles and distances from a point.
If your limits of integration (those numbers telling you where to start and stop) involve x² + y², that's a HUGE clue. Because x² + y² = r² in polar! It's like a giant flashing sign saying, "Go Polar!"
Let's Get Our Hands Dirty (Figuratively, Of Course)
Imagine you have an integral like this:
∫∫ √(x² + y²) dA
over a region that’s a perfect circle of radius 1. In Cartesian, that square root looks like it’s going to cause some serious headaches. You'd be stuck with trig substitution, and nobody really enjoys that unless they're a math masochist.
But in polar?
We know √(x² + y²) = r. Easy!

And our region is a circle of radius 1. So, r goes from 0 to 1.
And since it’s a full circle, θ goes from 0 to 2π.
So our integral transforms into:
∫₀²π ∫₀¹ r * (r dr dθ)
Which simplifies to:
∫₀²π ∫₀¹ r² dr dθ
See how much cleaner that is? That grumpy bear of an integral just turned into a fluffy bunny!
And integrating r² with respect to r? Piece of cake. You get r³/3. No sweat.
Then you plug in your limits for r (1 and 0), and you’re left with integrating a simple constant with respect to θ. And boom! You’ve got your answer.

The Quirky Side of Polar
Did you know that polar coordinates were actually invented by someone named Gregorio Fontana in the 17th century? Pretty cool, right? He probably looked at all those square shapes and thought, "There has to be a smoother way to describe things!"
And here’s a funny thought: in polar, you can actually have multiple representations for the same point. For example, (r, θ) is the same as (r, θ + 2π) or (r, θ - 2π). It’s like saying you’re at the same spot, just after you’ve done an extra lap around the block. A little bit of mathematical wiggle room!
Also, the origin (0,0 in Cartesian) is just (0, θ) for any angle in polar. It’s the ultimate free spirit of the coordinate plane!
Why is This So Darn Fun?
It’s fun because it’s about seeing things differently. It’s about finding the most elegant way to solve a problem. It’s like cracking a puzzle and realizing there was a simpler, more beautiful solution all along.
It's the thrill of transformation. Taking something that seems complicated and making it… manageable. Even elegant.
It’s the feeling of being a math ninja, using the right tool for the right job. And polar coordinates are definitely a cool tool to have in your arsenal.
So, next time you see an integral that’s making you sweat, take a peek. Does it look a bit… circular? Does it scream "I’d be happier with an angle and a radius"?
If so, don't be afraid to dive into the world of polar coordinates. You might just find that the math gets a whole lot more fun.
It’s not just about getting the right answer. It’s about enjoying the journey. And sometimes, that journey is best taken in a circle.
