Angle Pair Relationships With Parallel Lines Worksheet Answer Key
Hey there, math explorers! Ever found yourself staring at a worksheet, especially one about those wiggly lines called parallels, and thought, "Hmm, what's going on here?" If that's you, then you've probably stumbled into the super interesting world of angle pair relationships. And if you've been wrestling with a worksheet and are secretly (or not so secretly!) hoping for a peek at the answer key, well, you're in the right place. Let's dive in, nice and easy, and see why these relationships are actually pretty neat.
So, imagine you've got two lines that are like best friends – they run side-by-side forever and never, ever touch. We call those parallel lines. Think of train tracks, or the edges of a perfectly laid out road. Then, along comes a third line, a sort of interloper, that cuts across both of them. This line is called a transversal. It’s like a busy street crossing our parallel paths. Now, when this transversal crashes the party, it creates a bunch of angles. And that's where the magic happens!
These angles, born from the intersection of our parallel lines and the transversal, aren't just random numbers. Oh no, they've got a whole system going on. They're related! It's like they've got secret handshakes or insider information. We call these connections angle pair relationships. And understanding them is like getting a cheat code for solving geometry problems.
The "Secret Handshakes" of Angles
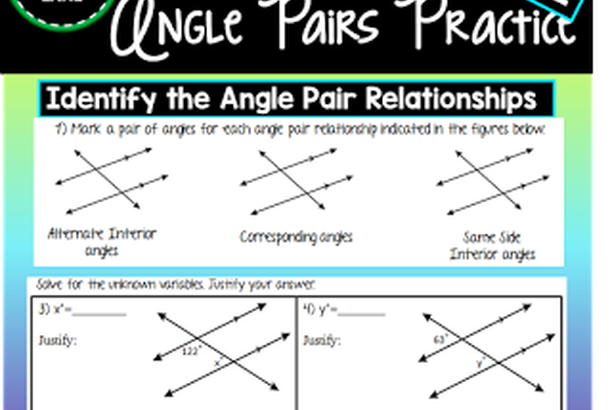
Let's talk about some of the most common and coolest of these relationships. First up, we have corresponding angles. Picture this: you've got your two parallel lines, and your transversal. Now, look at the angles that are in the same position at each intersection. If you were to slide the top intersection down perfectly onto the bottom one, these corresponding angles would land right on top of each other. Pretty neat, huh? And the coolest part? Corresponding angles are equal when the lines are parallel.
Think of it like this: imagine you're standing at a crossroads. The angle you make looking down one street on the left is like the angle someone at the other parallel crossroads makes looking down their corresponding street on the left. If the roads are parallel, those angles are going to be the same, right? No matter how far apart the crossroads are.
Next, let's meet the alternate interior angles. These guys are like the rebels of the group. They're on opposite sides of the transversal, and they're inside the parallel lines. So, they're tucked away in the middle. And get this: alternate interior angles are equal too, when the lines are parallel. They're doing their own thing, but still respecting the parallel rule.
![Parallel Lines Cut By A Transversal Worksheet [Free Printable]](https://brighterly.com/wp-content/uploads/2025/05/Parallel-Lines-Cut-By-A-Transversal-worksheet.png)
Imagine two people sitting at opposite ends of a long, parallel bench. If they both lean inward towards the center of the bench at the same angle, those leaning angles are alternate interior angles. They're on opposite sides of the "center line" (the transversal) but tucked in between the "bench" (the parallel lines). The fact that they're equal is kind of a cool symmetry.
Then there are the alternate exterior angles. These are the opposite of the interior ones. They're on opposite sides of the transversal, but they're outside the parallel lines. Think of them as the ones chilling on the outer edges. And guess what? Yep, you guessed it: alternate exterior angles are also equal when the lines are parallel.
It’s like two kids on opposite sides of a playground, each standing near the fence on the outside. If they both turn inwards towards the playground by the same amount, their angles relative to the fence would be equal. It's a bit of a mirrored effect happening on the outside.

Now, let's talk about the neighbours. Consecutive interior angles (sometimes called same-side interior angles) are on the same side of the transversal and are inside the parallel lines. Unlike their alternate interior cousins, these guys don't add up to the same value. Instead, consecutive interior angles are supplementary. This means they add up to 180 degrees. They're like a dynamic duo that complements each other perfectly.
Think of two people on the same side of that parallel bench again. If one leans slightly forward and the other leans slightly backward, they might balance each other out to a straight line (180 degrees). They're sharing the "straight line" vibe, but in different directions.
We also have vertical angles. These are the ones that are opposite each other where any two lines intersect. They're like those siblings who always seem to be doing the exact opposite thing, but in a way that’s perfectly balanced. Vertical angles are always equal, no matter what. They don't even need parallel lines for this trick!
And finally, linear pairs. These are two angles that sit next to each other and form a straight line. They are also supplementary, meaning they add up to 180 degrees. They're the perfect example of how two things can come together to create something simple and whole, like two puzzle pieces forming a straight edge.

Why This Stuff Matters (Besides the Worksheet!)
Okay, so why should you care about all these fancy angle names and their relationships? Well, beyond acing that worksheet (which, let's be honest, is a pretty good motivator!), understanding these relationships is the foundation for so much more in geometry. It's like learning your ABCs before you can read a novel.
When you're faced with a geometry problem, and you spot parallel lines and a transversal, your brain should immediately start buzzing with these relationships. You can use them to find unknown angles. If you know one angle, you can often figure out several others just by applying these rules. It’s like having a set of keys that can unlock many doors.
Imagine you’re building something, or designing something. Knowing how angles behave when lines are parallel can help you ensure things are aligned, balanced, and look just right. It’s the silent architect behind so many things we see around us.
The "Answer Key" Mindset
So, about that answer key. While it's tempting to just flip to the back and see the answers, the real fun, and the real learning, comes from understanding how to get there. Think of the answer key not as a shortcut, but as a confirmation. It's like checking your work after a cool experiment.
When you're working through a problem, and you're unsure, ask yourself: what kind of angles are these? Are they corresponding? Alternate interior? Vertical? Once you've identified the relationship, you can then apply the rule: are they equal? Do they add up to 180? This systematic approach is what makes these worksheets less daunting and more like a puzzle waiting to be solved.
Don't be afraid to draw on your worksheet, label angles, and even draw arrows to show relationships. Sometimes, a visual aid is all you need to see the connection. It's like giving yourself a little map to navigate the geometric landscape.
So, the next time you see a worksheet with parallel lines and transversals, don't just see a bunch of lines and numbers. See a system of relationships, a secret language of angles waiting to be deciphered. And remember, the best way to "get the answers" is to understand the journey. Happy angle hunting!
