Adding Subtracting And Multiplying Polynomials Worksheet Answers

Ever feel like you're wrestling with a giant, cryptic puzzle when it comes to math? Well, get ready to unlock a secret level of awesome because we're diving into the surprisingly fun world of adding, subtracting, and multiplying polynomials! Think of it less like tedious equations and more like a super-powered game of digital LEGOs. These operations are the building blocks for so many cool things in math and science, from graphing amazing curves to understanding how things grow and change. So, grab your virtual toolkit, because with a little practice and the right set of answers, you'll be a polynomial pro in no time!
Why Polynomials Are Your New Best Friends
Polynomials might sound intimidating, but they're actually just fancy ways of describing relationships between numbers and variables. They're like the secret language of graphs, representing everything from the path of a thrown ball to the projected growth of a business. Being able to add, subtract, and multiply them is your key to understanding and manipulating these relationships. It's like learning to speak fluent math! And honestly, there's a real satisfaction in conquering these skills. It's like solving a riddle and finding that perfect, elegant solution.
Think about it: ever wondered how a video game designer creates realistic explosions or how an engineer designs a bridge that can withstand tons of weight? Polynomials are often at the heart of these complex calculations. By mastering these fundamental operations, you're not just memorizing formulas; you're developing the ability to think critically, solve problems, and even create new things. It's a superpower that extends far beyond the classroom!
The Magic of the Worksheet Answers
So, where do adding, subtracting, and multiplying polynomials worksheet answers come into play? They're your trusty sidekicks on this math adventure! Imagine you're building something complex with LEGOs. You have the instructions, but sometimes, you need to see what the finished product looks like to make sure you're on the right track. That's precisely what worksheet answers do. They provide a benchmark, a guide, and a way to check your work.
When you're working through a set of problems, it's easy to get a little lost in the details. Did you combine the like terms correctly? Did you distribute that negative sign properly when subtracting? The answers are your instant feedback loop. They let you see where you might have made a tiny slip-up and, more importantly, they reinforce when you've nailed it! This immediate feedback is crucial for learning. It builds confidence and prevents you from practicing mistakes. Plus, the sheer joy of seeing a correct answer after a bit of head-scratching is a reward in itself!
Think of worksheet answers as your personal math coach, always there to give you a high-five when you're right and a gentle nudge when you need to adjust your approach.
Beyond just checking, having access to answers can actually make the learning process more efficient and less frustrating. Instead of spending hours stuck on a single problem, you can quickly identify areas where you need more practice. This allows you to focus your energy on the concepts that are still a bit fuzzy, rather than redoing problems you've already mastered. It's like having a shortcut to understanding, allowing you to progress faster and tackle even more exciting mathematical challenges.
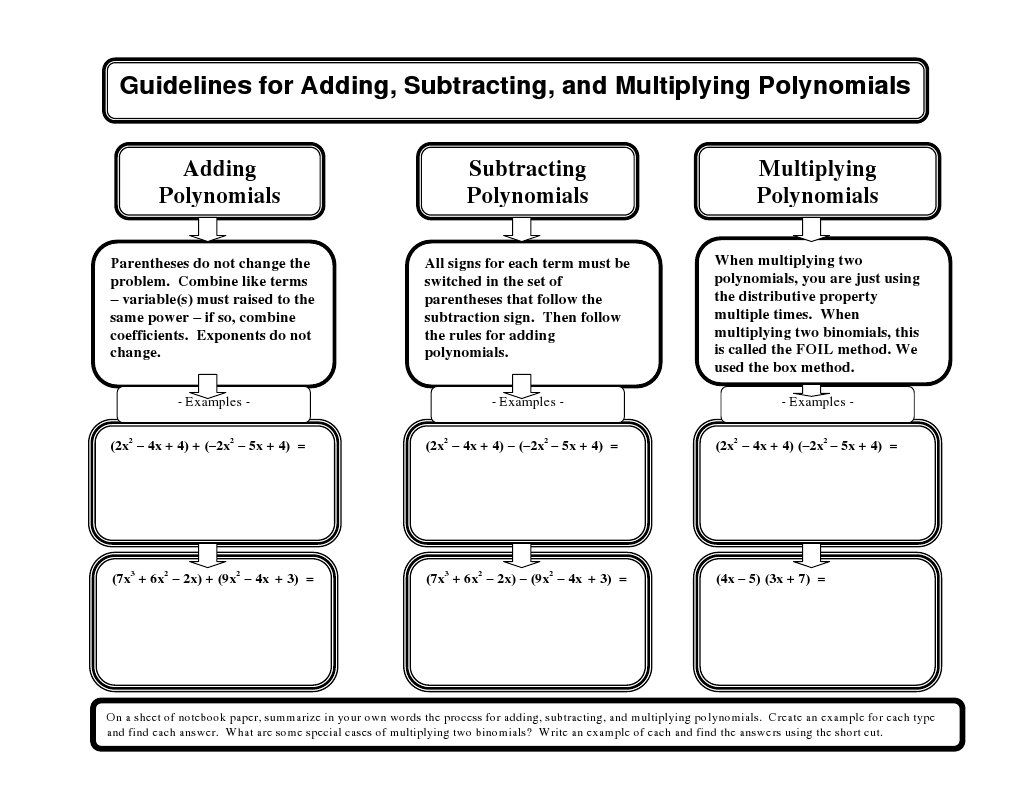
Adding Polynomials: Combining Like Terms
When we add polynomials, it's like gathering similar items. If you have 3 apples and someone gives you 2 more apples, you have 5 apples. In the world of polynomials, "apples" are like terms – terms with the same variable raised to the same power. So, if you have 3x² and you add 2x², you get 5x². Easy, right? We only add the coefficients (the numbers in front of the variables). If the terms aren't alike, they just hang out together. For example, 3x² + 2x stays as 3x² + 2x because you can't combine apples and oranges!
The process involves lining up the polynomials (often by powers of the variable) and then adding the coefficients of the like terms. It's a bit like sorting socks – you put all the blue ones together, all the red ones together, and so on. The worksheet answers are your ultimate sock-sorting check!

Subtracting Polynomials: The Crucial Minus Sign
Subtracting polynomials has a little twist: you have to be careful with that minus sign! When you subtract a polynomial, you're essentially distributing that negative sign to every term inside the parentheses. This means you change the sign of each term in the polynomial being subtracted. So, if you're subtracting (x + 2) from (3x - 5), it becomes 3x - 5 - x - 2. Now, it looks like an addition problem, and you can combine your like terms: (3x - x) + (-5 - 2) = 2x - 7.
This is where those worksheet answers are a lifesaver. It’s so common to forget to distribute the negative sign to every term. A quick check against the correct answer helps you catch this sneaky error and reinforces the importance of that little minus sign. It’s a small detail that makes a big difference!

Multiplying Polynomials: The Distributive Property Power-Up
Now for the fun part: multiplying polynomials! This is where the distributive property shines. You have to multiply each term in the first polynomial by each term in the second polynomial. Think of it like a chain reaction. If you're multiplying (x + 2) by (x + 3), you multiply 'x' by 'x', then 'x' by '3', then '2' by 'x', and finally '2' by '3'. This gives you x² + 3x + 2x + 6.
The final step is to combine any like terms, just like in addition. So, x² + 3x + 2x + 6 simplifies to x² + 5x + 6. There are different methods, like the FOIL method (First, Outer, Inner, Last) which is specifically for multiplying two binomials, or the box method, which can be super helpful for larger polynomials. Again, the worksheet answers are your trusty guide to ensure you've correctly applied all those multiplications and combined your terms!
Mastering these operations is a fundamental step in your math journey. And with the help of adding, subtracting, and multiplying polynomials worksheet answers, you can navigate this process with confidence and a smile. Happy polynomial wrangling!
