Adding Scalar Multiples Of Vectors Graphically Mastering Physics
Hey there, physics fans and curious minds! Ever feel like math can be a bit… dry? Like you’re staring at numbers and symbols that just don’t do anything? Well, get ready to have your mind blown, because we’re diving into a corner of physics that’s surprisingly fun and incredibly visual: adding scalar multiples of vectors graphically. Sounds fancy, right? But trust me, it’s more like playing with magical arrows and making them do your bidding.
Imagine you have a bunch of these things called vectors. Think of them as arrows. They have a direction and a length. They’re not just abstract ideas; they represent real things in the world! Like, say, a push on a box, the path of a ball, or even your journey to the coffee shop this morning. Pretty cool, huh?
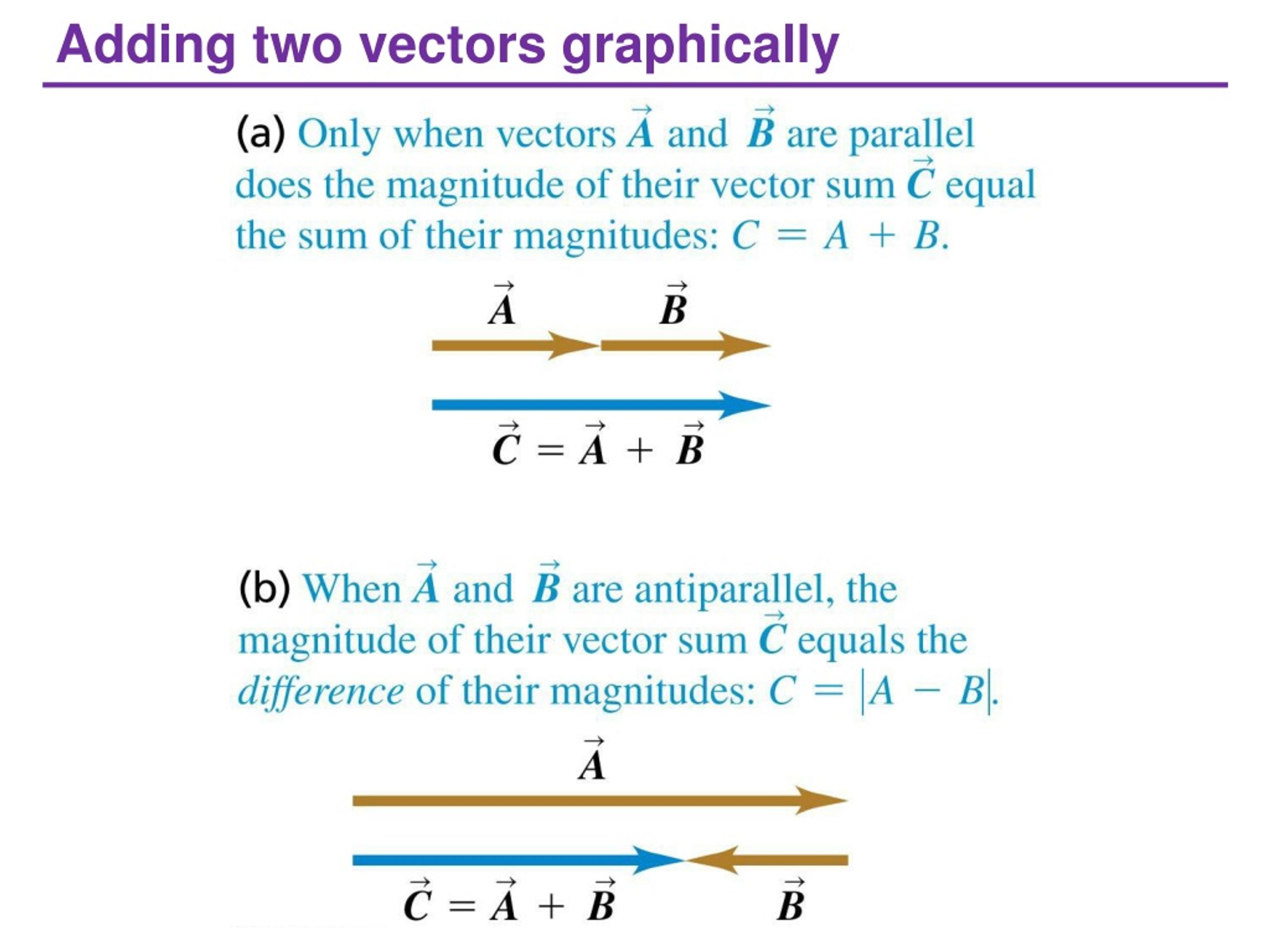
Now, what if you wanted to change one of these arrows? Maybe make it twice as long, pointing in the same direction? Or flip it around and make it half its original size? That’s where scalar multiples come in. A scalar is just a regular number. When you multiply a vector by a scalar, you’re basically telling that arrow to stretch, shrink, or even flip its direction. It’s like giving your arrow superpowers!
So, let’s say you have an arrow, let’s call it vector A. If you multiply vector A by a number, like 2, you get a new arrow that’s twice as long as vector A but points in the exact same direction. Easy peasy! If you multiply vector A by -1, you get an arrow the same length, but it points in the completely opposite direction. Boomerang effect, anyone?
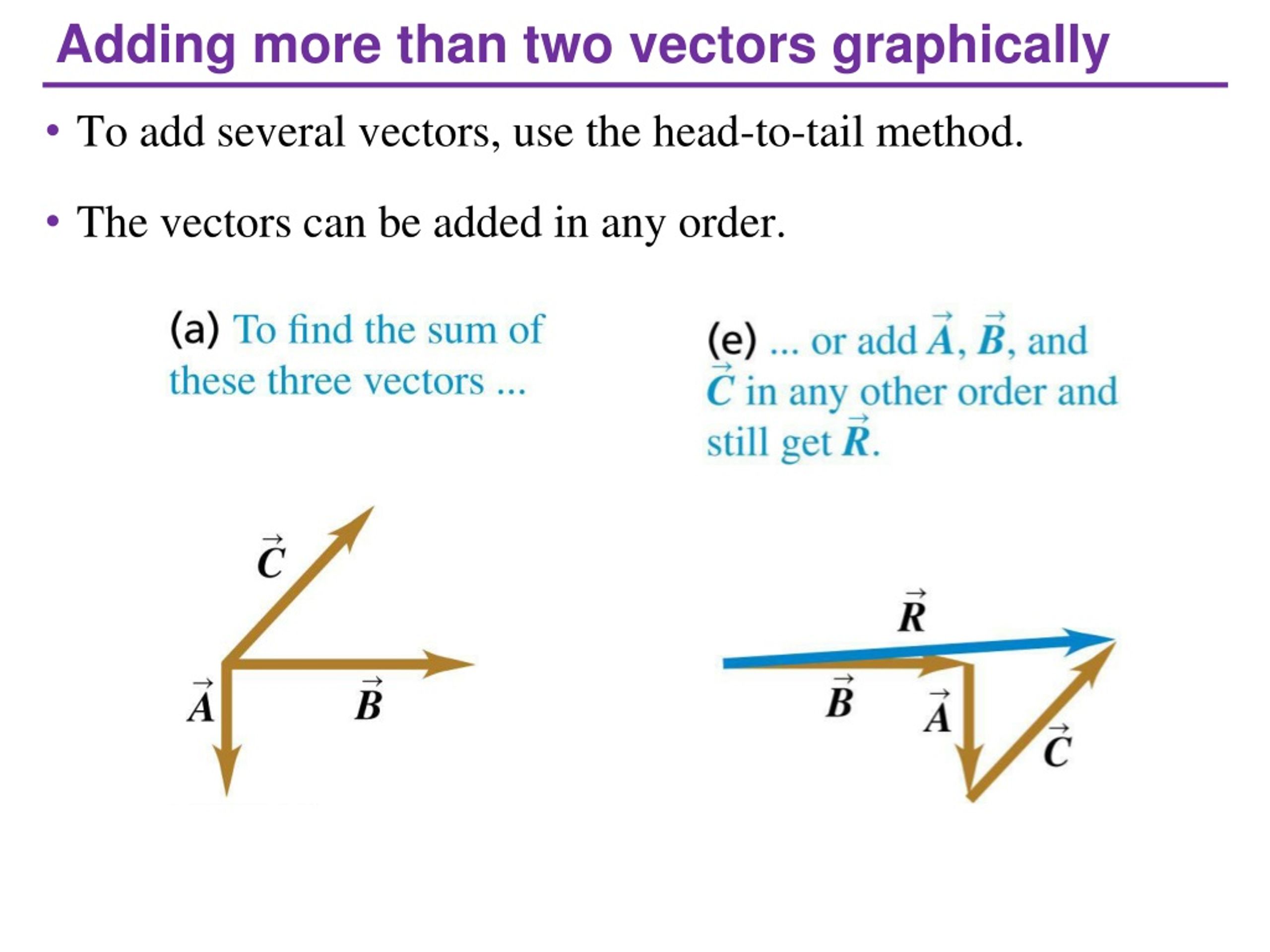
But here's where the real magic happens: adding vectors. And not just any vectors, but these modified ones, these scalar multiples! Imagine you have one arrow representing you walking 5 blocks east, and another arrow representing your friend walking 3 blocks north. If you want to know where you both end up relative to your starting point, you need to add those arrows. And doing it graphically? That's the fun part.
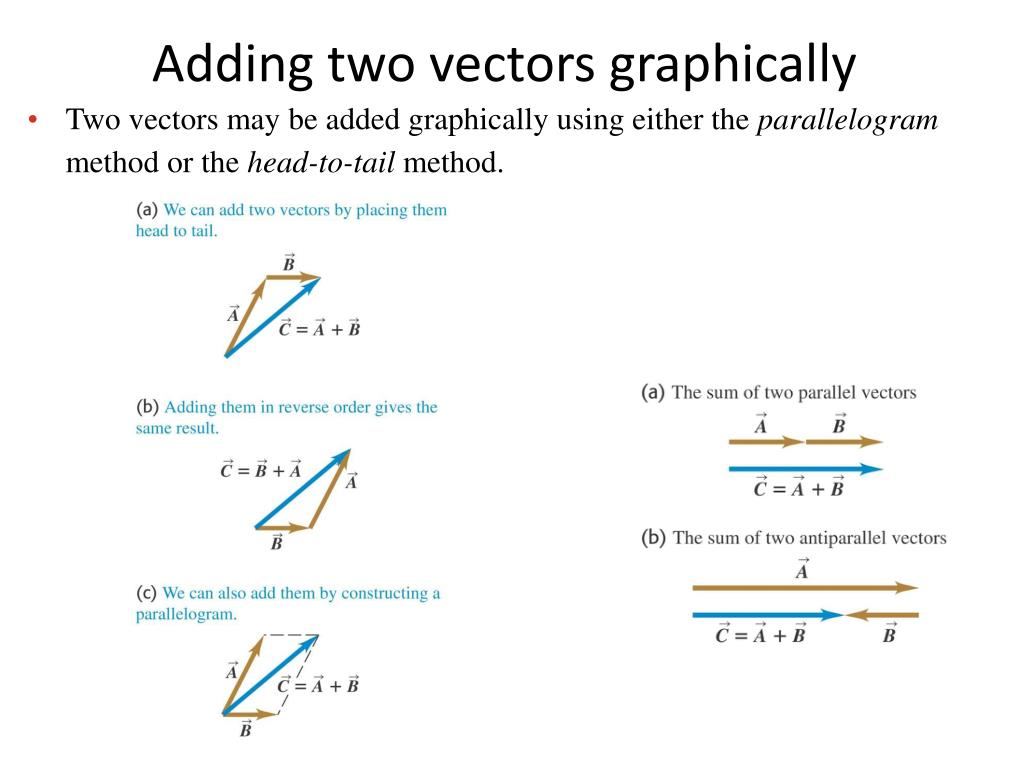
Instead of messy equations, you’re drawing! You draw your first arrow. Then, from the tip of that first arrow, you draw your second arrow. Where the second arrow ends is where the combined effect takes you. It’s like tracing your path on a map. You walk here, then you walk there, and the final arrow shows you the shortcut back home!
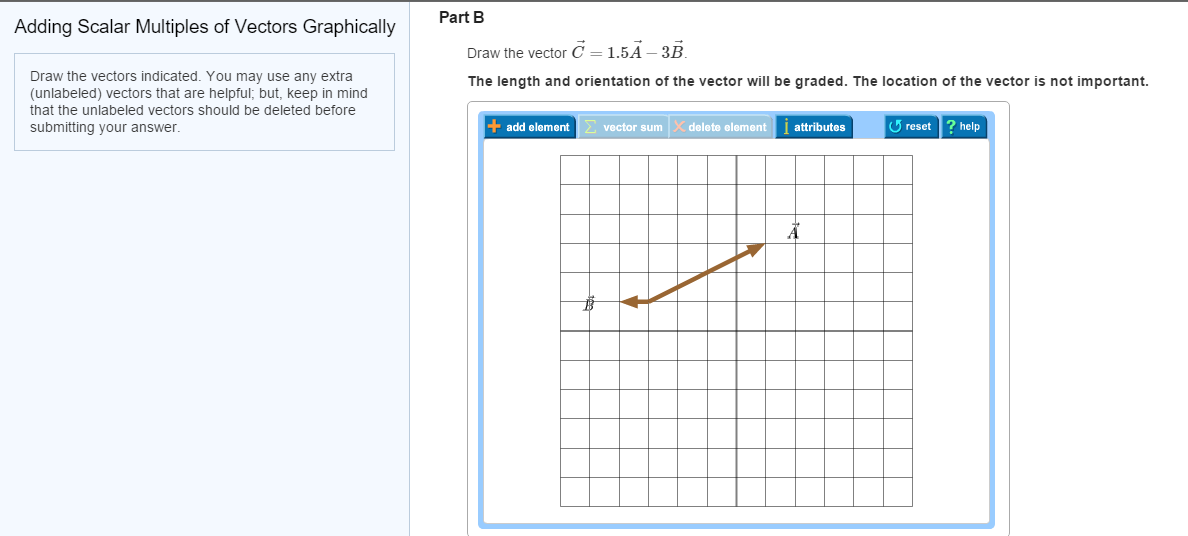
Now, let’s bring in those scalar multiples. Suppose you have an arrow vector B, and you decide you want to take a longer trip in that direction. So, you multiply vector B by, say, 3. You've now got this super-sized arrow. Then, you have another arrow, vector C, and you decide to go in its direction, but only half as far. So, you multiply vector C by 0.5.

The exciting part is that you can then add this scaled-up vector B to this scaled-down vector C, all using the same drawing trick. Draw the first modified arrow. Then, from its tip, draw the second modified arrow. Voilà! The resulting arrow from the start of the first to the end of the second shows you the combined outcome of your scaled-up adventure and your scaled-down exploration. It’s like orchestrating a ballet of arrows, each with its own length and direction, and seeing where they all land together.
What makes this so special? It’s the intuition it builds. You can see what’s happening. You’re not just crunching numbers; you’re visualizing the forces, the movements, the journeys. It’s like having a superpower that lets you predict how things will combine and interact in the real world, just by sketching it out. It’s this tangible connection to abstract concepts that makes mastering physics feel less like a chore and more like a game.
Think about it: you’re not just solving a problem; you’re drawing a story. A story of forces pushing, of paths weaving, of destinations reached. And the more you practice, the more natural it becomes. The arrows start to dance on your paper, and the solutions emerge effortlessly. It’s a beautiful blend of art and science, where your creativity can directly lead you to understanding complex physical phenomena.
The elegance of the graphical method for adding scalar multiples of vectors is that it bypasses a lot of the potential confusion that can arise with complex calculations. You can grasp the core idea of how these scaled and combined vectors behave without getting bogged down in algebraic steps. It’s like getting the gist of a movie by looking at the poster and trailers, but then being able to predict the entire plot with amazing accuracy just by sketching a few key scenes.
So, if you’ve ever looked at physics and thought, “This is way too complicated for me,” I urge you to give this a try. Grab a piece of paper, a ruler, and a protractor (or just eyeball it if you're feeling bold!). Start with simple vectors and scalars, and then gradually increase the complexity. You’ll be amazed at how quickly you can start to understand and even predict how different forces or movements will combine. It’s an incredibly rewarding way to build your physics intuition, and frankly, it's just a whole lot of fun.
It’s a reminder that sometimes, the most profound understanding comes not from staring intently at equations, but from looking at the world around us and seeing the arrows at play. And with adding scalar multiples of vectors graphically, you get to be the artist, the conductor, and the physicist, all at once. Pretty neat, right?
