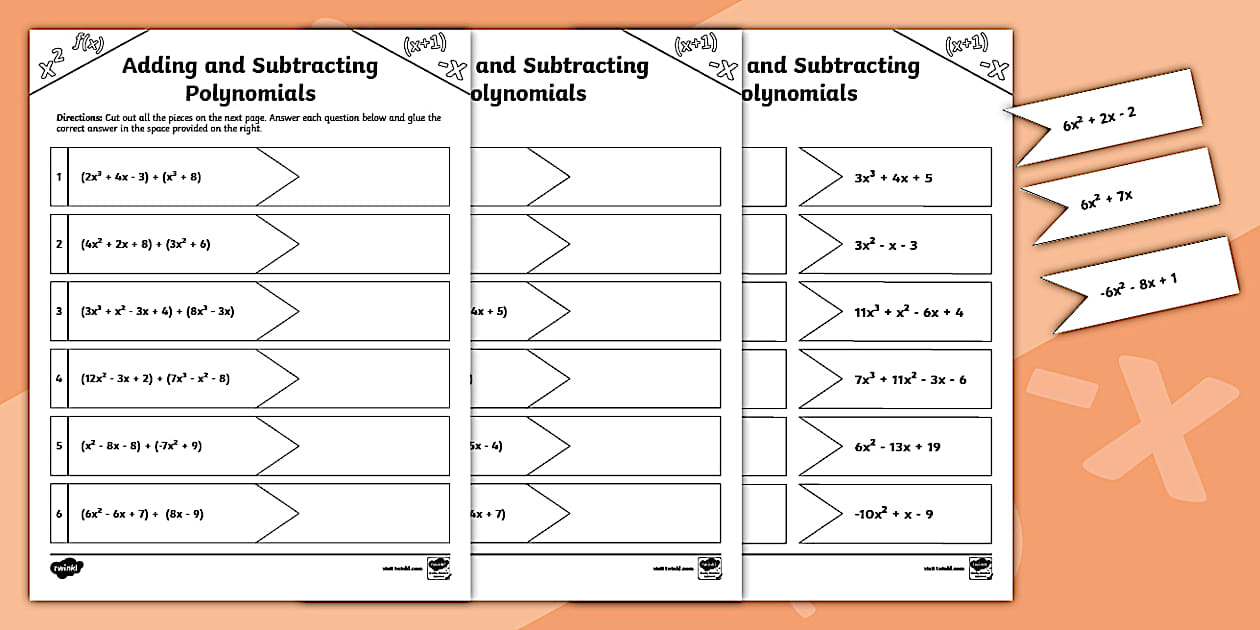
Adding And Subtracting Polynomials Puzzle Worksheet Answers

Hey there, math adventurer! So, you've been wrestling with polynomials, huh? Like trying to sort a giant box of mismatched socks. Totally get it. And now you've stumbled upon this magical thing called an "Adding and Subtracting Polynomials Puzzle Worksheet." Ooh, fancy! But here's the real kicker, right? You've done the work, you've scribbled all over it, and now you're staring at it, probably with a slightly panicked look, and thinking... "Wait, are these answers actually right?!" Because, let's be honest, math can be a sneaky beast sometimes. One tiny sign error and your whole beautifully crafted answer turns into a hot mess. Been there, done that, bought the t-shirt.

And that's where we come in! Think of me as your friendly neighborhood math helper, the one who's spilled enough ink on these things to know a thing or two. We're not about to dive into a super formal, lecture-y kind of vibe. Nah, we're just going to chat about these puzzle worksheets, and more importantly, the answers. Because, let's face it, the puzzle is fun, but confirming you've actually solved the puzzle? That's the real victory, wouldn't you agree?

So, what are we even talking about when we say "adding and subtracting polynomials"? It sounds so… official. But it's really not that scary, promise! It's like grouping similar things together. You know, like putting all your red socks in one pile, all your blue socks in another. With polynomials, our "socks" are the terms with the same variable and the same exponent. Simple, right? We call those like terms. It's all about finding those buddies and adding or subtracting their coefficients. Easy peasy, lemon squeezy!

Now, when these puzzle worksheets pop up, they're usually designed to be a little bit of a game. They're not just asking you to solve a bunch of problems; they want you to use those answers to decode something. Maybe it's a funny joke, a secret message, or even just a cool phrase. It's like a treasure hunt for your brain! And if your answers are off? Well, that treasure is going to stay buried, and nobody wants that. That’s why checking those puzzle worksheet answers is crucial.

So, How Do We Even Get These Answers?

Let's do a quick refresher, just for kicks. Imagine you have two polynomials. Polynomial number one might be something like, 3x² + 2x - 5. And polynomial number two, let's make it a bit different, maybe -x² + 4x + 1. Now, if we're adding them, we just line them up and combine the like terms. The x² terms go together, the x terms go together, and the plain old numbers (we call those constants, fancy, huh?) go together.

So, for our example, (3x² + 2x - 5) + (-x² + 4x + 1) becomes:

• x² terms: 3x² + (-x²) = 2x² (See? We're just adding the numbers in front.)
• x terms: 2x + 4x = 6x (This one's pretty straightforward.)
• Constants: -5 + 1 = -4 (Watch out for those negative signs, they're tricky!)

And BAM! Our combined polynomial is 2x² + 6x - 4. Ta-da! See? Not so bad. It's like adding ingredients for a recipe. You just make sure you're putting the flour with the flour, and the sugar with the sugar.

Adding And Subtracting Polynomials Worksheet With Answer Key

Now, subtraction is where things can get a little more interesting. It's like adding, but with a twist. When you subtract a polynomial, you're essentially distributing a negative sign to every term inside the parentheses you're subtracting. Think of it as flipping the sign of each term in the second polynomial. So, if we were subtracting our second polynomial from the first: (3x² + 2x - 5) - (-x² + 4x + 1), we'd first rewrite it as 3x² + 2x - 5 + x² - 4x - 1. See how the signs flipped? The -x² became +x², the +4x became -4x, and the +1 became -1. It's like a little mathematical magic trick!

Once you've done that sign-flipping, you just add them up like we did before!

• x² terms: 3x² + x² = 4x²
• x terms: 2x + (-4x) = -2x
• Constants: -5 + (-1) = -6

So, the result of our subtraction is 4x² - 2x - 6. Phew! See? It’s all about those little steps. And if you're doing a puzzle worksheet, you'll take each of these resulting polynomials and match them up with a letter or a number to reveal your clue. Pretty cool, right?

Why the Puzzle Aspect is Actually Pretty Smart

I know, I know. Sometimes those puzzles can feel a little like busywork. But honestly, they're a super clever way to make sure you're actually paying attention to your answers. If you just solved a bunch of random problems, you might not double-check them as rigorously. But when there's a joke or a message on the line? Suddenly, you're way more motivated to get it right. It's like bribing yourself with a good laugh or a neat piece of trivia. Who knew math could be so… motivating?

Adding and Subtracting Polynomials Matching Puzzle Worksheet

And think about it. When you're doing addition and subtraction of polynomials, the most common errors come from two places:

1. Confusing like terms: Trying to add an x² to an x? Nope, that's a no-go.
2. Sign errors: Especially during subtraction, where you have to flip those signs. These little guys are the absolute worst offenders.

The puzzle format forces you to confront both of these potential pitfalls. If your answer is wrong, the joke won't make sense, or the message will be gibberish. And that, my friend, is a pretty clear sign that it's time to go back and re-examine your work. It’s like having a built-in error checker that doesn't judge you (much!).

So, You've Got Your Answers. Now What?

Alright, so you've soldiered through the worksheet, you've got a list of polynomial answers, and maybe even a jumbled-up message. This is the moment of truth! Most puzzle worksheets will have a key, right? It'll say something like: "Match your answer to the problem number, and write the corresponding letter." So, if problem #1's answer is 2x² + 6x - 4, and next to that problem, it says "A", then you write "A" in the blank space for #1 in the puzzle solution. Simple, right?

But here's the real secret sauce to making sure your "Adding And Subtracting Polynomials Puzzle Worksheet Answers" are spot on: double-checking your work, and then triple-checking it. I know, I know, it sounds like a drag. But trust me, it's way less of a drag than realizing at the very end that you got the whole darn thing wrong because of one misplaced minus sign. It's like building a house of cards. One wrong placement and the whole thing tumbles down. Not ideal.

When you're checking, go back to the original problems. Grab a different colored pen – that's my favorite trick. It helps your brain see it with fresh eyes. Reread the problem carefully. Did you add or subtract? Did you distribute that negative sign correctly? Are you sure you combined all the like terms?

Algebra I: Adding and Subtracting Polynomials Square Puzzle

Let's Talk About Those Tricky Bits

Okay, let's get a little more specific. Sometimes, the polynomials you're adding or subtracting are written in a slightly different order. For example, you might have 5x - 2x² + 3 and -6x + 7x² - 1. See how the terms aren't in the standard "descending order of exponents" format? That's where things can get confusing. My advice? Always rewrite them in standard form first. It makes it SO much easier to see the like terms.

So, 5x - 2x² + 3 becomes -2x² + 5x + 3. And -6x + 7x² - 1 becomes 7x² - 6x - 1. Now you can add them neatly:

• x² terms: -2x² + 7x² = 5x²
• x terms: 5x + (-6x) = -x
• Constants: 3 + (-1) = 2

Result: 5x² - x + 2. Much cleaner, right? It's all about making it as easy for yourself as possible. We're not here to make math harder than it needs to be.

Another classic stumble block? When one of the polynomials is missing a certain type of term. For example, adding (4x² + 3) and (2x³ - 5x). Notice that the first polynomial is missing an x³ term, and the second is missing an x² and a constant term. When you're lining them up, it's helpful to put in a placeholder with a zero coefficient. So, 4x² + 3 can be thought of as 0x³ + 4x² + 0x + 3. And 2x³ - 5x can be 2x³ + 0x² - 5x + 0.

Adding and Subtracting Polynomials Worksheet No 2 (with solutions

Then you add them:

• x³ terms: 0x³ + 2x³ = 2x³
• x² terms: 4x² + 0x² = 4x²
• x terms: 0x + (-5x) = -5x
• Constants: 3 + 0 = 3

Result: 2x³ + 4x² - 5x + 3. See? That little zero placeholder is like a friendly hand guiding you through the process. It prevents those awkward moments where you might accidentally add an x² to an x³ or something equally silly. And nobody wants to be that person, do they?

The Joy of Finding the Right Answers

Honestly, there’s a certain satisfaction that comes from solving one of these puzzle worksheets correctly. It’s like finding the last piece of a jigsaw puzzle. That moment when the joke finally makes sense, or the secret message is revealed, and you realize, "YES! I DID IT!" It's a small victory, maybe, but it's a victory nonetheless. And in the sometimes-daunting world of algebra, those victories are worth celebrating.

So, if you’re staring at your "Adding And Subtracting Polynomials Puzzle Worksheet Answers" and feeling a little unsure, take a deep breath. Go back through your work, one problem at a time. Use that colored pen. Look for those pesky sign errors. Make sure your like terms are truly like terms. You've got this!

And remember, if you're really stuck, don't be afraid to ask for help. A teacher, a tutor, a classmate who seems to have their life (and their polynomials) together – they're all great resources. But before you do that, give it one more solid shot. You might surprise yourself with what you can figure out when you just put your mind to it. Happy puzzling, and may your answers be ever so correct!